Question

How do you solve and graph $3y + 6 \leqslant 2y$?

Answer 1

Hint: In this question, the linear equation in one variable is given. Any linear equation in- one variable can be represented in the form of $ax + b = 0$. Where a, and b are real numbers and ‘a’ is not equal to 0. We will first treat it as equality and find the equation of the line by plotting any two points on it. Now, we will just shade the region accordingly and get the required region.

Complete step by step solution:
In this question, the given linear equation in one variable is as below.
$ \Rightarrow 3y + 6 \leqslant 2y$
First, let us subtract 3y on both sides.
$ \Rightarrow 3y - 2y + 6 \leqslant 2y - 2y$
The subtraction of 3y and 2y is y on the left-hand side, and the subtraction of 3y and 2y is 0 on the right-hand side.
Therefore,
$ \Rightarrow y + 6 \leqslant 0$
 Let us subtract 6 on both sides.
 $ \Rightarrow y + 6 - 6 \leqslant 0 - 6$
The subtraction of 6 and 6 is 0 on the left-hand side, and subtraction of 0 and 6 is -6 on the right-hand side. That is equal to,
$ \Rightarrow y \leqslant - 6$
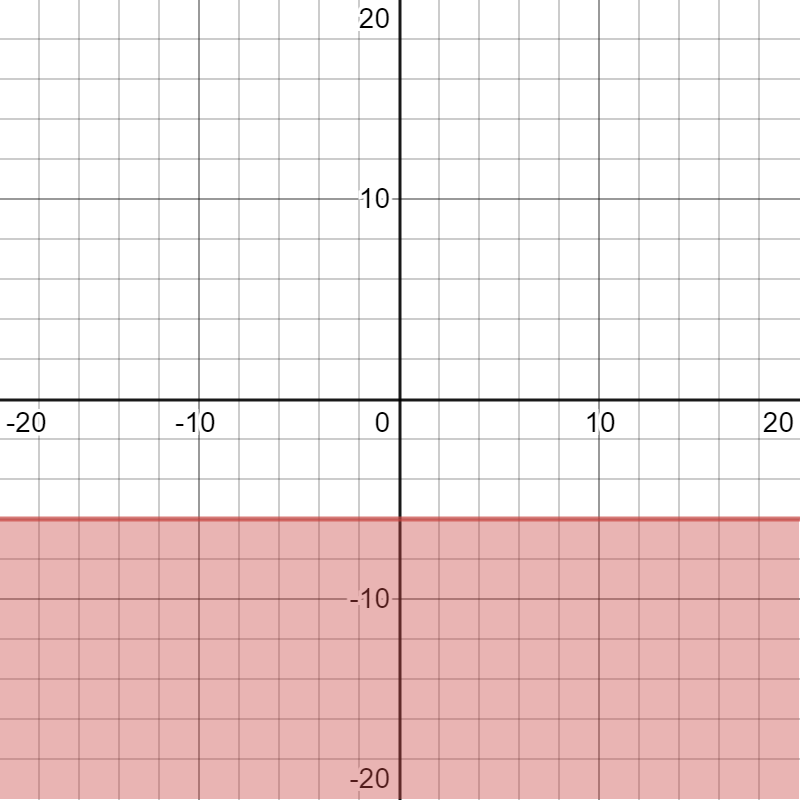
To graph this equation, we will draw a horizontal line at -6 on the vertical axis. The line will be a solid line because the inequality operator contains an “or equal to” clause. We will shade below the line because the inequality operator also contains a “less than” clause.

Note:
We first treated the given inequality as equality because we first needed to find the boundary line of the graph and after finding the boundary line; we just see where the graph intends to be. To check whether we have to shade inwards towards the origin or outwards, you should just put the origin in the given inequality and if we get the correct result, we shade inwards, otherwise outwards.