Question

How do you solve and graph \[2x > - 10\] and \[9x < 18\]

Answer 1

Hint:Here in this question, we have to plot a graph. Usually while plotting the graph, we plot x axis versus y- axis. But here in this question we have only one variable and we have greater than and less than inequality. For this variable we have to plot the graph. Hence, we get a line. We cannot specify a particular point.

Complete step by step explanation:
The graph is generally plotted x- axis versus y -axis. When we have two variables then we plot a two-dimensional graph. Here in this question, we have only one variable but this is also a two-dimensional graph. Here y is not mentioned. Here in this question we have two inequalities. First we simplify the given inequality and we plot graph for the inequality.
Consider the first inequality
\[2x > - 10\]
Divide the above equation by 2
\[ \Rightarrow x > - 5\]
Consider the second inequality
\[9x < 18\]
Divide the above equation by 9
\[ \Rightarrow x < 2\]
For any value of y either it is positive terms or the negative terms the value of x will ranges from the -5 to 2
The graph for the given equation \[2x > - 10\] and \[9x < 18\] is as shown below.

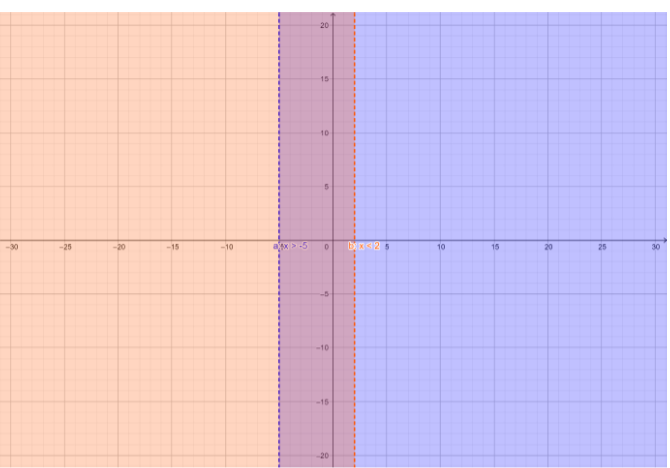
If we see the graph the region is parallel to the y-axis and it does not have a specified line.
We don’t have a one dimensional graph, if the equation contains only one variable either its x or y we must know that for any value x or y the equation will be constant.

Note: The graph is plotted against the two axes namely X-axis and Y-axis. If we know the value of one, we can find the other by using the equation of the graph. This graph is two dimensional because they have mentioned only two axes. The value of y can range, it does not have a particular value. Because the inequality has greater than and less than symbols.