Question

How do you solve and draw the graph $\dfrac{2x}{3} >4x+10$?

Answer 1

Hint: We try to take points which have x coordinates that satisfies $\dfrac{2x}{3}>4x+10$. There is no restriction on the y coordinates. Based on the points we try to find the space or region in the 2-D plane which satisfies $\dfrac{2x}{3}>4x+10$. We multiply with 3 and solve to get the required interval.

Complete step-by-step solution:
The inequation $\dfrac{2x}{3}>4x+10$ represents the space or region in 2-D plane where the x coordinates of points satisfy $\dfrac{2x}{3}>4x+10$.
We can solve the inequation treating them as equations for the operations like addition and subtraction. In case of multiplication and division we need to watch out for the negative values as that changes the inequality sign.
We first take some points for the x coordinates where $\dfrac{2x}{3}>4x+10$.
We multiply with 3 to both sides of the inequality.
$\begin{align}
  & 3\times \dfrac{2x}{3}>3\left( 4x+10 \right) \\
 & \Rightarrow 2x>12x+30 \\
\end{align}$
Now we take the variables on one side and get
$\begin{align}
  & 2x>12x+30 \\
 & \Rightarrow 2x-12x>30 \\
 & \Rightarrow -10x>30 \\
\end{align}$
Now we divide with negative number $-10$ and get
\[\begin{align}
  & \dfrac{-10x}{-10}<\dfrac{30}{-10} \\
 & \Rightarrow x<-3 \\
\end{align}\]
The interval is $x<-3$.

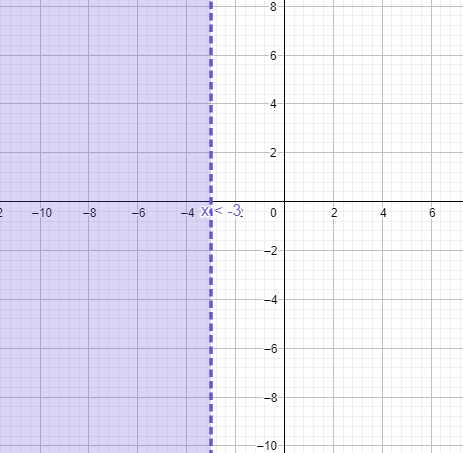
Note: We can also express the inequality as the interval system where $\dfrac{2x}{3}>4x+10$ defines that $x\in \left( -\infty ,-3 \right)$. The interval for the y coordinates will be anything which can be defined as $y\in \left( -\infty ,\infty \right)$. We also need to remember that the points on the line $\dfrac{2x}{3}>4x+10$ will not be the solution for the inequation.