Question

How do you solve $3x+4y=-11$ and $7x-5y=3$ using substitution?

Answer 1

Hint: We have been given two linear equations in 2-variables, variable-x and variable-y which must be solved simultaneously to find the point of intersection of the two given lines. In order to find this point of intersection by the substitution method, we shall substitute the value of variable-x from the first equation to the second equation. After obtaining the value of y-variable, we shall substitute this value in the first equation to calculate the value of x-variable.

Complete step by step answer:
Given that
$3x+4y=-11$ ……………… equation (1)
And $7x-5y=3$ ……………… equation (2)
In equation (1), we shall transpose the term with the y-variable to the right hand side and obtain this equation in terms of x-variable which will be further substituted into equation (2).
$\Rightarrow 3x=-11-4y$
Dividing both sides by 3, we get
$\Rightarrow x=\dfrac{-11-4y}{3}$
Substituting this value of x-variable in equation (2), we get
$\Rightarrow 7\left( \dfrac{-11-4y}{3} \right)-5y=3$
Opening the brackets on the left hand side and multiplying each term by 7, we get
$\Rightarrow \left( \dfrac{-77-28y}{3} \right)-5y=3$
Taking LCM on the left hand side and solving more, we get
$\Rightarrow \dfrac{-77-28y-15y}{3}=3$
$\Rightarrow -77-28y-15y=9$
Here, we shall transpose the constant term, -77 to the right hand side and add it to 9.
$\Rightarrow -28y-15y=9+77$
$\Rightarrow -43y=86$
Dividing both sides by -43 to obtain the y-coordinate of the point of intersection, we get
$\Rightarrow y=-\dfrac{86}{43}$
$\Rightarrow y=-2$
Now, we shall substitute the value of y-variable in equation (1) to obtain the value of x-coordinate.
$\Rightarrow 3x+4\left( -2 \right)=-11$
$\Rightarrow 3x-8=-11$
Transposing the constant term, -8 to the right hand side, we get
$\Rightarrow 3x=-11+8$
$\Rightarrow 3x=-3$
Dividing both sides by 3, we get
$\Rightarrow x=-1$

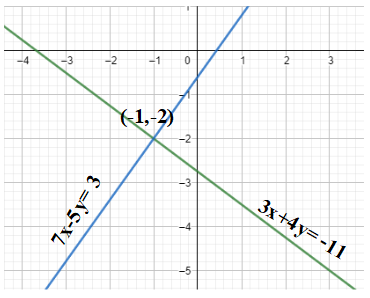
Therefore, the solution or the point of intersection of $3x+4y=-11$ and $7x-5y=3$ is $\left( -1,-2 \right)$.

Note: Another method of finding the solution or the point of intersection of the given linear equations in two variables was by sketching the graph of both the straight-lines on the same cartesian plane. However, we must take care while marking the points on the graph. The possible mistake which can be made while sketching the graph would be marking (0,2) instead of (0,-2).