Question

How do you solve $0={{x}^{2}}+4x+4$ graphically and algebraically?

Answer 1

Hint: To solve the given equation graphically we will plot the graph of the given equation and find the point of intersection. The x-coordinate of intersection point is the solution of the given equation. To solve the given equation algebraically we will use the splitting the middle term method.

Complete step by step solution:
We have been given an equation $0={{x}^{2}}+4x+4$.
We have to solve the given equation graphically and algebraically.
First let us solve the given equation algebraically. For this we will use the splitting the middle term method. Now, by splitting the middle term of the given equation we will get
\[\begin{align}
  & \Rightarrow {{x}^{2}}+4x+4=0 \\
 & \Rightarrow {{x}^{2}}+2x+2x+4=0 \\
\end{align}\]
Now, taking the common factors out we will get
\[\begin{align}
  & \Rightarrow x\left( x+2 \right)+2\left( x+2 \right)=0 \\
 & \Rightarrow \left( x+2 \right)\left( x+2 \right)=0 \\
\end{align}\]
Now, putting each factor equal to zero and simplifying further we will get
$\Rightarrow x+2=0$ and $\Rightarrow x+2=0$
$\Rightarrow x=-2$ and $\Rightarrow x=-2$
Now, to solve the given equation graphically let us draw a graph of the given equation.
Let the given equation is $y={{x}^{2}}+4x+4$
When we draw a parabola we get that the parabola touches the x axis at $x=-2$.

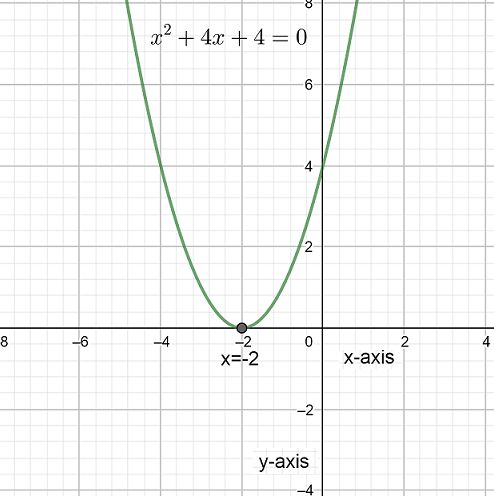
So $x=-2$ is the only solution of the given equation.

Note: The point to be noted is that if the leading coefficient of the parabola is positive the parabola will be opening upwards. If the leading coefficient is negative then the parabola will be opening downwards. If the discriminant value is zero then the parabola only cut the x-axis.