
What is the solution set of the inequality $5 - \left| {x + 4} \right| \leqslant - 3$ ?
Answer
474.9k+ views
Hint: Here we are going to find the solution to the given inequality by using usual addition, subtraction on both sides of the inequality. The absolute value function takes any negative or positive term and transforms it to its positive form.
Complete step by step answer:
Given a set of inequality is $5 - \left| {x + 4} \right| \leqslant - 3$----------(1)
First, subtract $5$ from each side of the inequality to isolate the absolute value term while keeping the inequality balanced.
$ \Rightarrow 5 - \left| {x + 4} \right| - 5 \leqslant - 3 - 5$
Simplifying it we get,
$ \Rightarrow - \left| {x + 4} \right| \leqslant - 8$
Now by making the positive terminal of both terms the inequality by multiply each side of the inequality by $ - 1$ to remove the negative sign from the absolute value term while keeping the inequality balanced. However, because we are multiplying or dividing by a negative term we must also reverse the inequality term,
$ \Rightarrow - 1 \times \left( { - \left| {x + 4} \right|} \right) \leqslant - 1 \times \left( { - 8} \right)$
Now we get,
$ \Rightarrow \left| {x + 4} \right| \geqslant 8$
The absolute value function takes any negative or positive term and transforms it to its positive form. Therefore, we must solve the term within the absolute value function for both its negative and positive equivalent,
$ \Rightarrow - 8 \geqslant x + 4 \geqslant 8$
Now, subtract $4$ from each segment of the system of inequalities to solve for $x$ ,
Keeping the system balanced, we get,
$ \Rightarrow - 8 - 4 \geqslant x + 4 - 4 \geqslant 8 - 4$
On simplifying it we get,
$ \Rightarrow - 12 \geqslant x + 0 \geqslant 4$
$ \Rightarrow - 12 \geqslant x \geqslant 4$
This solution set of $x$ can be seen in the below diagram, where the orange color represents the solution set.
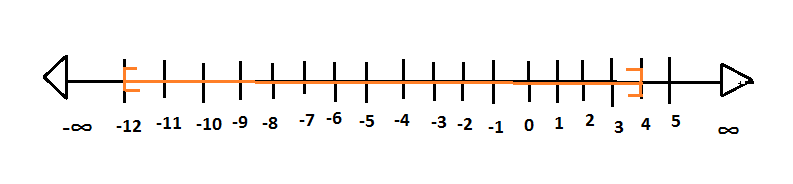
Therefore, the solution set of the inequality $5 - \left| {x + 4} \right| \leqslant - 3$ is $ - 12 \geqslant x \geqslant 4$.
Note:
This is an inequality where the solution to an absolute value equation is pointed, the solution to an absolute value inequality is going to be intervals. In this inequality asked to find the $x$ values that belong to which interval. They are asking you for the $x$ values that will make the absolute value expression greater than a negative number. Since the absolute value will always be greater than any negative number, the solution must be all $x$ or all real numbers.
Complete step by step answer:
Given a set of inequality is $5 - \left| {x + 4} \right| \leqslant - 3$----------(1)
First, subtract $5$ from each side of the inequality to isolate the absolute value term while keeping the inequality balanced.
$ \Rightarrow 5 - \left| {x + 4} \right| - 5 \leqslant - 3 - 5$
Simplifying it we get,
$ \Rightarrow - \left| {x + 4} \right| \leqslant - 8$
Now by making the positive terminal of both terms the inequality by multiply each side of the inequality by $ - 1$ to remove the negative sign from the absolute value term while keeping the inequality balanced. However, because we are multiplying or dividing by a negative term we must also reverse the inequality term,
$ \Rightarrow - 1 \times \left( { - \left| {x + 4} \right|} \right) \leqslant - 1 \times \left( { - 8} \right)$
Now we get,
$ \Rightarrow \left| {x + 4} \right| \geqslant 8$
The absolute value function takes any negative or positive term and transforms it to its positive form. Therefore, we must solve the term within the absolute value function for both its negative and positive equivalent,
$ \Rightarrow - 8 \geqslant x + 4 \geqslant 8$
Now, subtract $4$ from each segment of the system of inequalities to solve for $x$ ,
Keeping the system balanced, we get,
$ \Rightarrow - 8 - 4 \geqslant x + 4 - 4 \geqslant 8 - 4$
On simplifying it we get,
$ \Rightarrow - 12 \geqslant x + 0 \geqslant 4$
$ \Rightarrow - 12 \geqslant x \geqslant 4$
This solution set of $x$ can be seen in the below diagram, where the orange color represents the solution set.
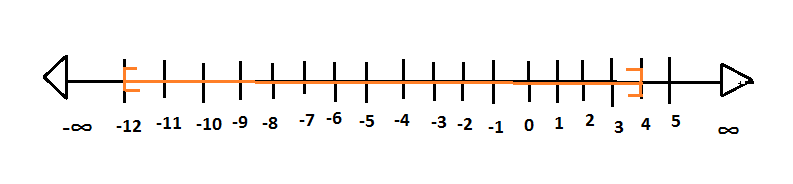
Therefore, the solution set of the inequality $5 - \left| {x + 4} \right| \leqslant - 3$ is $ - 12 \geqslant x \geqslant 4$.
Note:
This is an inequality where the solution to an absolute value equation is pointed, the solution to an absolute value inequality is going to be intervals. In this inequality asked to find the $x$ values that belong to which interval. They are asking you for the $x$ values that will make the absolute value expression greater than a negative number. Since the absolute value will always be greater than any negative number, the solution must be all $x$ or all real numbers.
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE

10 examples of friction in our daily life




