
What is the solution of the inequality, ${{x}^{2}}<25$?
Answer
524.1k+ views
Hint: The most common and easy method to solve an inequality is by taking all the terms from both sides of the equation and putting them in one side, such that, one of the sides becomes equal to zero. Then we try to factorize our expression and use the number line system to find the range of values that satisfies the condition given in the problem.
Complete step-by-step solution:
We have been given in the problem to solve the inequality: ${{x}^{2}}<25$
We will first of all rearrange all the terms on one side of the equation. This can be done as follows:
$\Rightarrow {{x}^{2}}-25<0$
Now, the second step in the process of solving an inequality is to see if the given expression can be factorized or not. Here, the expression can be factorized. This can be done as follows:
$\Rightarrow (x-5)(x+5)<0$
The above expression has been factored. Now, we will find the points where the function is equal to zero. We can see from our above expression that there are two points where this function is equal to zero. These two points are:
$\Rightarrow x=-5,5$
Now, we will use the number line method to find the range of values for which our function is less than zero. This is done as follows:
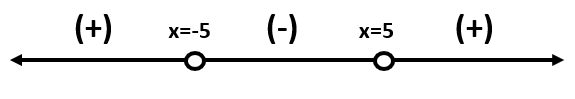
In the above number line system, we can see that the function is less than zero in between -5 and 5. This can be written as $\left( -5,5 \right)$ .
Hence, the solution of the inequality, ${{x}^{2}}<25$, comes out to be $\left( -5,5 \right)$.
Note: Whenever we write, the final solution of any inequality. The big brackets “[]” are used for when both the terms in the bracket are included. The small brackets “()” is used for when none of the two terms are included and curly brackets “{}” are used to write answers in the form of a set where only each value is the answer.
Complete step-by-step solution:
We have been given in the problem to solve the inequality: ${{x}^{2}}<25$
We will first of all rearrange all the terms on one side of the equation. This can be done as follows:
$\Rightarrow {{x}^{2}}-25<0$
Now, the second step in the process of solving an inequality is to see if the given expression can be factorized or not. Here, the expression can be factorized. This can be done as follows:
$\Rightarrow (x-5)(x+5)<0$
The above expression has been factored. Now, we will find the points where the function is equal to zero. We can see from our above expression that there are two points where this function is equal to zero. These two points are:
$\Rightarrow x=-5,5$
Now, we will use the number line method to find the range of values for which our function is less than zero. This is done as follows:
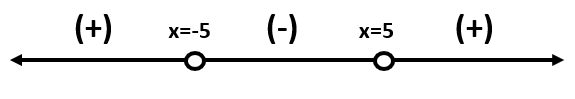
In the above number line system, we can see that the function is less than zero in between -5 and 5. This can be written as $\left( -5,5 \right)$ .
Hence, the solution of the inequality, ${{x}^{2}}<25$, comes out to be $\left( -5,5 \right)$.
Note: Whenever we write, the final solution of any inequality. The big brackets “[]” are used for when both the terms in the bracket are included. The small brackets “()” is used for when none of the two terms are included and curly brackets “{}” are used to write answers in the form of a set where only each value is the answer.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




