Question

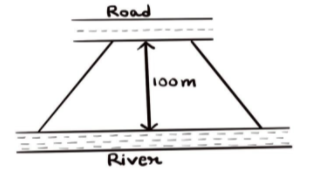
Sohan wants to buy a trapezium shaped field. Its sides along the river are parallel to and twice the sides along the road. If the area of this field is $10500 sqmetre$ and the perpendicular distance between the two parallel sides is $100m$ , find the length of the side along the river.

Answer 1

Hint: Use the formula for the area of a trapezium to get the length of the side along the river. The formula of the area of a trapezium is: Area= $\dfrac{1}{2} \times height \times (a + b)$ where $a$ and $b$ are the two parallel sides. In this question, the two parallel sides are the side along the road and the side along the river.

Complete step-by-step answer:
Let the length of the side parallel to the road be $a$.
Let the length of the side parallel to the side of the river be $b$.
So from the question, we can say that $b = 2a$.
The following information is also given in the question.
The height of this field is $100m$ and the area is $10500 sqmetre $.
Substituting these values in the formula for area of a trapezium we get,
Area of the trapezoidal field= $\dfrac{1}{2} \times height \times (a + b)$
$
   \Rightarrow 10500 = \dfrac{1}{2} \times 100 \times (a + b) \\
   \Rightarrow 10500 = 50 \times (a + 2a) \\
   \Rightarrow 10500 = 50 \times 3a \\
   \Rightarrow 3a = \dfrac{{10500}}{{50}} \\
   \Rightarrow a = \dfrac{{10500}}{{50 \times 3}} \\
   \Rightarrow a = 70m \\
 $
Therefore, the length of the side along the river is:
$
  b = 2a \\
   \Rightarrow b = 2 \times 70 = 140m \\
 $
So the length of the side along the river is $140m$.

Note: Make sure that you do not go wrong with the formula of the area of the trapezium. Identify the parallel sides correctly. If by mistake you take the two other sides, the answer will be wrong. Also, be careful about what the question is asking. Do not stop after finding the value of $a$.