Question

Snow is falling vertically at a constant speed of \[3m/s\] At what angle from the vertical do the snowflakes appear to be falling as viewed by the driver of a car traveling on a straight level road with a speed of \[60km/h\] ? (In degrees)

Answer 1

Hint: We are asked to find the angle at which the snowflakes appear to be falling. We can start to answer this question by writing down the given data along with an appropriate diagram and finding the relative speed of the snowflake with respect to the car and then using the formula.
Formulas used: The relative velocity of the snowflake is given by the formula, \[{v_{AB}} = {v_A} - {v_B}\]
The tangent from the figure we draw is given by the formula, \[\theta = {\tan ^{ - 1}}\dfrac{{{v_c}}}{{{v_s}}}\]
Where A and B are two bodies

Complete answer:
Let us start by noting down the data given in the question,
The speed at which snow is falling is given as, \[{v_s} = - 3m/s\]
The speed at which the car is moving is given as, \[{v_c} = 60km/h\]
We need to convert this into the same unit as the speed of the snowflake. We can do this by
\[{v_c} = 60 \times \dfrac{5}{{18}} = - \dfrac{{150}}{9}m/s\]
Moving onto the diagram part,

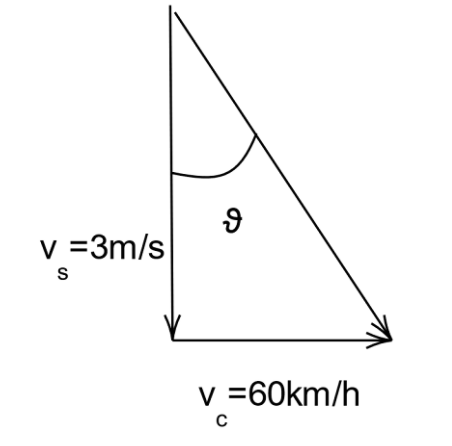
We can find the angle at which the snowflake is falling by using the formula, \[\theta = {\tan ^{ - 1}}\dfrac{{{v_c}}}{{{v_s}}}\]
Now we can substitute the values and get \[\theta = {\tan ^{ - 1}}\dfrac{{{v_c}}}{{{v_s}}} = {\tan ^{ - 1}}\dfrac{{150}}{{9 \times 3}} = 79.78\]
Hence, we have found the angle at which the snowflakes appear to be falling with respect to the driver in the car.
The snowflake will appear to fall at a speed of \[{v_{AB}} = {v_A} - {v_B} = - 3j - \dfrac{{150}}{9}i\]
We use the direction notations to show that the direction of the movement of the snow and car are different

Note:
Relative velocity of two bodies with respect to each other is given by the formula
\[{v_{AB}} = {v_A} - {v_B}\]
This gives us the relative velocity of body A with respect to body B.