Question

What is the slope and y-intercept of this line $8x+6y=12$ ?

Answer 1

Hint: From the question, we have been asked to find the slope and y intercept of $8x+6y=12$
We can find the slope and intercept of the given equation by converting the given equation into \[y=mx+b\] form.
In this \[y=mx+b\] form of the equation,
\[b\] is your \[y\]intercept and,
\[m\] is your slope.
Now, as a process, we have to convert the given equation into \[y=mx+b\] form.

Complete step by step solution:
From the question, we have been given that,
$\Rightarrow 8x+6y=12$
Now, take away 12 from both sides of the given equation.
By taking away 12 from both sides of the equation, we get the below equation,
$\Rightarrow 8x+6y-12=12-12$
$\Rightarrow 8x+6y-12=0$
Now, rearrange the equation into the form of \[y=mx+b\].
By rearranging the obtained equation into \[y=mx+b\] form, we get the below equation,
$\Rightarrow 6y=-8x+12$
$\Rightarrow y=-\dfrac{8}{6}x+\dfrac{12}{6}$
$\Rightarrow y=-\dfrac{4}{3}x+2$
Now, we can clearly observe that the equation is in the form of \[y=mx+b\].
Now, compare the coefficients of both the equations to get the slope of the equation.
By comparing the coefficients, we get
Slope of the equation $=m=-\dfrac{4}{3}$.
Now, we have to find the y intercept.
 let us find the\[y\] intercept.
$\Rightarrow y=-\dfrac{4}{3}x+2$
When the line crosses the\[y\] axis, \[x\] is at zero, so we can use\[x=0\] to find\[y\] intercept.
$\Rightarrow y=-\dfrac{4}{3}\left( 0 \right)+2$
$\Rightarrow y=2$
Therefore, we got the \[y\] intercept.
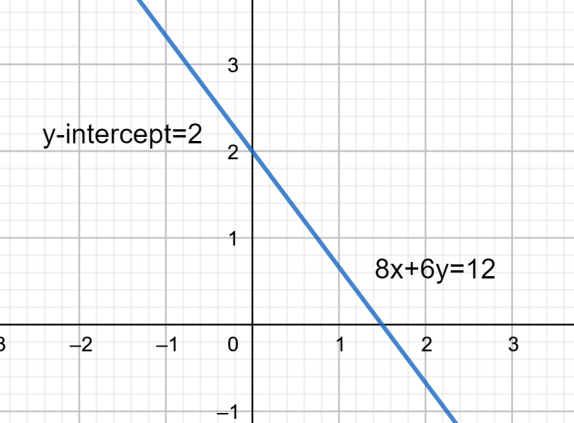
The figure will be as follows.

Note: Students should be well aware of the concept of slope and intercept. Students should be very careful while converting the given equation into slope intercept form. Also, students should be very careful while doing the calculation of finding the intercepts. Also, students should be careful while finding the slope of the given equation.