Question

What is the slope and y – intercept of the line \[x=-6\]?

Answer 1

Hint: For solving this question you should know about the slope of a line and the y – intercept of a line. If the point is given at x – axis then we will see the change at that axis. If the change occurs there then there will be any slope which we will count by the calculation but if there is no change or \[\Delta x=0\] then it has no slope and it will never cut the y – axis also.

Complete step by step solution:
According to the question it is asked that the line is \[x=-6\] and we have to calculate the slope and the y – intercept of this line.
If we find the y – intercept then it is found where the line in question crosses the y – axis (vertical axis), or when our x in a coordinate point is 0, such as (0, y) the slope is found by the change inn y / change in x.
The slope intercept form is \[y=mx+b\] where m is the slope and b is the y – intercept.
If we find a slope, then take any two points along the line or two given points, for example (3, 6) and (5, 7). The change in y is going to be \[{{y}_{2}}-{{y}_{1}}\] or in case of 7 – 6 which is equal to one.
Then we calculate our change in k which is done in the same way but with x – variables. \[{{x}_{2}}-{{x}_{1}}\] or in a case of 5 – 3 it will be equal to 2.
Therefore, for example our slope will be \[\dfrac{\Delta y}{\Delta x}\], and here
\[\Delta y={{y}_{2}}-{{y}_{1}}=1\]
And \[\Delta x={{x}_{2}}-{{x}_{1}}=2\]
So, the slope is equal to \[\dfrac{1}{2}\].
If we take our question then the point \[x=-6\], and only y is not given so the point is (-6, 0).
So, the change in the x values is equal to zero. And change in the y – value is also equal to zero.
So, the x is not intersecting the y. Thus, it does not have a y – intercept at all. And the gradient is undefined. And the slope is undefined.
So, the slope of \[x=-6\] is undefined and the y – intercepts are zero.

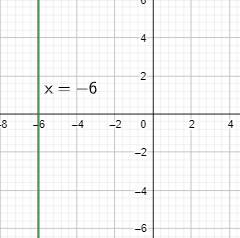
Note: The Y – intercepts of any line only occurs when the x intersects to the y. And if that is not intersecting or cutting to that then it will not any y – intercepts there. And if the change in x values of any equation of line is equal to zero then the slope of that line is always undefined value.