Question

Sketch the solution to the system of inequalities.
\[y<\dfrac{1}{2}x+2\]
\[y<-2x-3\]
(A)
   

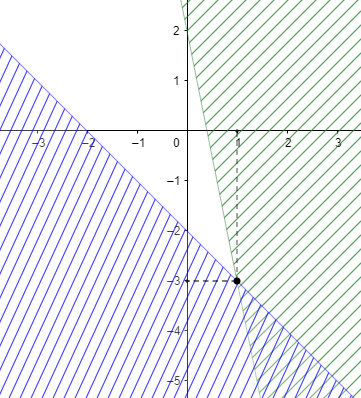
(B)
  

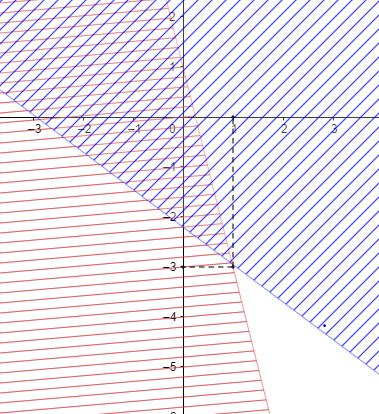
(C)

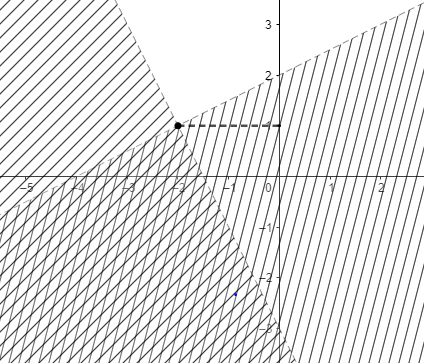
(D)

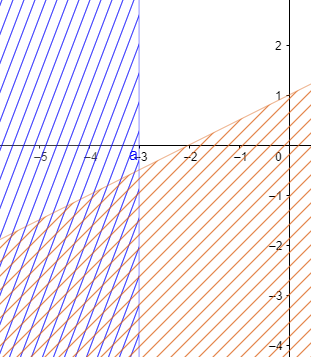
Answer 1

Hint: We are given a system of inequalities and we have to draw the graph of the given equations and so we have to select the most appropriate graphs given to us as options. We will begin by plotting the graph of the given equations and while plotting we will consider the equations as, \[y=\dfrac{1}{2}x+2\] and \[y=-2x-3\]. We will take points of these equations by keeping one of the variables as zero at a time. After plotting the graphs of the given equations, we will take a point as a reference and check if it fits the given inequality and accordingly we will have the solution set of the equation under consideration. Hence, we will have the graph of the given inequalities.

Complete step by step answer:
According to the given question, we are given a system of inequalities in which we have to draw the graph and then we will have to choose the most appropriate option from the given.
The system of inequalities that we have are,
\[y<\dfrac{1}{2}x+2\]
\[y<-2x-3\]
Firstly, we will be plotting the given inequalities and for that we will take the equations as,
\[y=\dfrac{1}{2}x+2\]
\[y=-2x-3\]
For each of the equations, we will take points to be plotted and for that we will let one of the variable be 0 and obtain the value of the other variable,
For \[y=\dfrac{1}{2}x+2\],
Putting \[x=0\], we get,
\[y=\dfrac{1}{2}(0)+2=2\]
The coordinate we get is \[\left( 0,2 \right)\]
Now, putting \[y=0\], we get,
\[0=\dfrac{1}{2}x+2\]
Solving for ‘x’, we get,
\[\Rightarrow \dfrac{1}{2}x=-2\]
\[\Rightarrow x=-4\]
The coordinate we get is, \[\left( -4,0 \right)\]

Similarly, for the equation \[y=-2x-3\],
Putting \[x=0\], we get,
\[y=-2\left( 0 \right)-3=-3\]
The coordinate we obtain is \[\left( 0,-3 \right)\].
Now, putting \[y=0\], we get,
\[-2x-3=0\]
Solving for ‘x’, we get.
\[\Rightarrow -2x=3\]
\[\Rightarrow x=\dfrac{3}{-2}=-1.5\]
The coordinate that we obtain is \[\left( -1.5,0 \right)\].
We have the graph as,

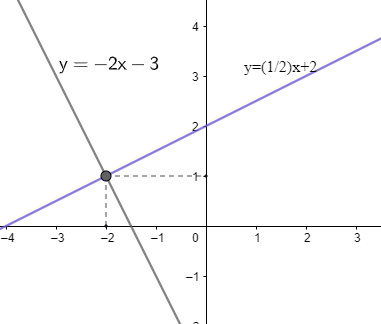
Now, in order to get the solution set, we will take a point as a reference for the both the inequalities given to us, we will take the origin, which is \[(0,0)\] and check for the correctness of the inequality which will further determine the solution of the equation.
We will substitute \[(0,0)\] in both the equations and check the inequality if it is right or not.
Substituting \[(0,0)\], we get,
\[y<\dfrac{1}{2}x+2\]
\[\Rightarrow 0<\dfrac{1}{2}(0)+2\]
\[\Rightarrow 0<2\] which is correct. So, the solution set is towards the origin.
For the inequality, \[y<-2x-3\]
\[\Rightarrow 0<-2(0)-3\]
\[\Rightarrow 0<-3\]
Which is incorrect, so the solution set for this inequality is away from the origin.
So, the solution set of the two inequalities is as follows,

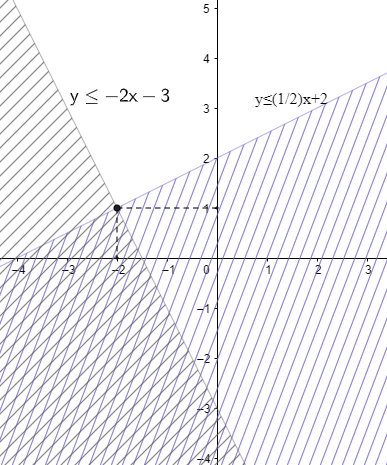
So, the correct answer is “Option C”.

Note: While plotting the graph first, the inequality should not be there in the expression else there is a possibility of getting the graph wrong. Only after plotting, when the solution area is to be determined, we make use of the inequality signs and check with a reference point the direction of the solution of the particular equation under consideration.