Question

How do you sketch the graph of $y={{\log }_{2}}x+3$ ?

Answer 1

Hint: At first, we convert the base $2$ to some standard base like $e$ or $10$ using the formula ${{\log }_{a}}m=\dfrac{{{\log }_{b}}m}{{{\log }_{b}}a}$ . After that, we perform some basic arithmetic operations and get an equation of the form $y=m\ln x+c$ . This can easily be plotted.

Complete step by step solution:
The given equation that we have is,
$y={{\log }_{2}}x+3....\left( 1 \right)$
At first, it may seem easy to plot the graph of the equation. But, if we observe carefully, we see that the base of the logarithm used here is $2$ . The standard bases of logarithms that we can plot using a graphing calculator are $e$ and $10$ . So, we first need to change the base $2$ to some standard base to plot the graph. For this problem, we choose the base $e$ .
Now, we know the formula of logarithms that ${{\log }_{a}}m=\dfrac{{{\log }_{b}}m}{{{\log }_{b}}a}$ . In our problem, we need to transform the logarithm ${{\log }_{2}}x$ so, we have, $m=x,a=2,b=e$ . Thus putting the values in the formula, we get,
$\Rightarrow {{\log }_{2}}x=\dfrac{{{\log }_{e}}x}{{{\log }_{e}}2}$
Now, we know that logarithm with base $e$ can be written as $\ln $ instead of ${{\log }_{e}}$ . So, implementing the said in the above equation, we get,
$\Rightarrow {{\log }_{2}}x=\dfrac{\ln x}{\ln 2}$
Putting the above value of ${{\log }_{2}}x$ in equation $\left( 1 \right)$ , we get,
$\Rightarrow y=\dfrac{\ln x}{\ln 2}+3$
Multiplying both sides of the above equation by $\ln 2$ , we get,
$\Rightarrow y\times \ln 2=\left( \dfrac{\ln x}{\ln 2}+3 \right)\times \ln 2$
This upon simplification gives,
\[\Rightarrow y\times \ln 2=\left( \ln x+3\ln 2 \right)\]
The value of $\ln 2$ is $0.693$ . Putting this value in the above equation, we get,
\[\Rightarrow y\times 0.693=\ln x+3\times 0.693\]
Simplifying, we get,
\[\Rightarrow 0.693y=\ln x+2.079\]
Dividing both sides by $0.693$ ,
\[\Rightarrow y=1.443\ln x+3....\left( 2 \right)\]
This is of the standard form $y=m\ln x+c$ . Thus, the graph is,

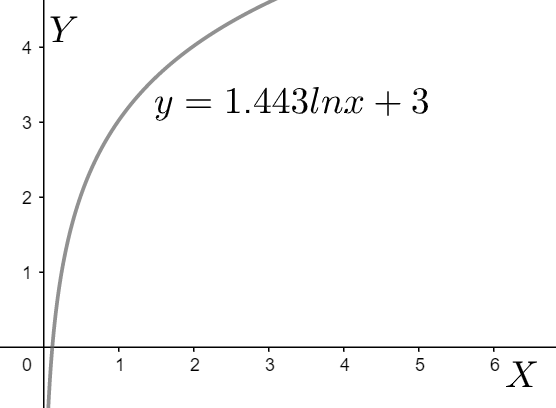
Note: We must be careful to notice the base as $2$ and should not blindly take it as $e$ or $10$ . Also, if we convert the base to $10$ or $e$ , we should stick to it. We can also solve by expression equation $\left( 2 \right)$ as $x={{e}^{\dfrac{y-3}{1.443}}}$ which will also give the same result.