
How do you sketch the graph of $y=-3{{x}^{2}}$ and describe the transformation?
Answer
541.8k+ views
Hint: The given problem is a simple demonstration of coordinate geometry of sub topic parabola. For plotting the graphs, we require a knowledge of graph theory and functions as well. For sums like these we first of all need to rearrange the equation in such a way that it represents one of the general equations of a parabola. Some of the general equations of the parabola are as follows.
Complete step by step solution:
Now we start off with the solution of the problem by writing that,
We first of all rearrange our given problem as,
${{x}^{2}}=-\dfrac{y}{3}$
Now, we make a transformation or in other words we can say that we change the variable to some other variables for the time being in such a way that the problem equation becomes similar to that of one of the general equations.
For the transformation, we can write,
\[Y=x,X=y\]
The equation hence transforms to,
\[{{Y}^{2}}=-\dfrac{X}{3}\]
Now, we can very clearly observe that the above equation looks similar to that of the equation \[{{y}^{2}}=4ax\], where a is $-\dfrac{1}{12}$ .
Thus, we plot our graph having a vertex of \[\left( 0,0 \right)\] . The nature of the graph will be same but, it will be narrower. At last, we replace the assumed coordinates with the original ones, that is Y with x and X with y.
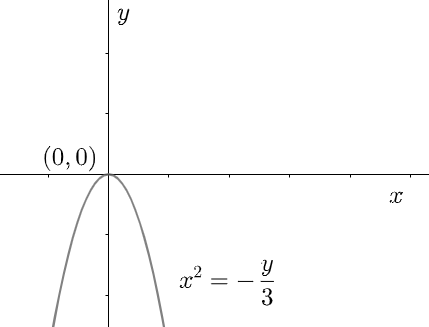
Note: For problems like these we need to be very thorough and fluent in functions as well as graph theory. While transforming an equation or shifting its origin we need to be very careful because, once we shift the origin of the function, we must also revert back to the original coordinate system after all our calculations have been done. Also, for times of need, we should also remember that when we transform or shift the origin form \[\left( 0,0 \right)\] to some point \[\left( a,b \right)\] , then all the other points also get shifted by \[\left( a,b \right)\] .
| Equation | Vertex | Foci |
| \[{{y}^{2}}=4ax\] | \[\left( 0,0 \right)\] | \[\left( a,0 \right)\] |
| \[{{y}^{2}}=-4ax\] | \[\left( 0,0 \right)\] | \[\left( -a,0 \right)\] |
| \[{{x}^{2}}=4by\] | \[\left( 0,0 \right)\] | \[\left( 0,b \right)\] |
| \[{{x}^{2}}=-4by\] | \[\left( 0,0 \right)\] | \[\left( 0,-b \right)\] |
Complete step by step solution:
Now we start off with the solution of the problem by writing that,
We first of all rearrange our given problem as,
${{x}^{2}}=-\dfrac{y}{3}$
Now, we make a transformation or in other words we can say that we change the variable to some other variables for the time being in such a way that the problem equation becomes similar to that of one of the general equations.
For the transformation, we can write,
\[Y=x,X=y\]
The equation hence transforms to,
\[{{Y}^{2}}=-\dfrac{X}{3}\]
Now, we can very clearly observe that the above equation looks similar to that of the equation \[{{y}^{2}}=4ax\], where a is $-\dfrac{1}{12}$ .
Thus, we plot our graph having a vertex of \[\left( 0,0 \right)\] . The nature of the graph will be same but, it will be narrower. At last, we replace the assumed coordinates with the original ones, that is Y with x and X with y.

Note: For problems like these we need to be very thorough and fluent in functions as well as graph theory. While transforming an equation or shifting its origin we need to be very careful because, once we shift the origin of the function, we must also revert back to the original coordinate system after all our calculations have been done. Also, for times of need, we should also remember that when we transform or shift the origin form \[\left( 0,0 \right)\] to some point \[\left( a,b \right)\] , then all the other points also get shifted by \[\left( a,b \right)\] .
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE

10 examples of friction in our daily life




