Question

How do you sketch the graph of \[y=0.5{{\left( x-2 \right)}^{2}}-2\] and describe the transformation?

Answer 1

Hint: In order to find the solution of the given question that is to find how to sketch the graph of \[y=0.5{{\left( x-2 \right)}^{2}}-2\] and describe the transformation, determine the form of the given equation with the help of the standard formula that is \[y=a{{\left( x-h \right)}^{2}}+k\] then determine the turning point that is find \[\left( h,k \right)\] by comparing the given equation with the standard formula that is \[y=a{{\left( x-h \right)}^{2}}+k\]. Now find the \[y\]-intercept by putting \[x=0\], factorise the equation and solve for \[y\]and also find the \[x\]-intercept by putting \[y=0\], factorise the equation and solve for \[x\]. After getting these points you’ll be able to sketch the graph and describe the transformation.

Complete step by step solution:
According to the question, given equation in the question is as follows:
\[y=0.5{{\left( x-2 \right)}^{2}}-2...\left( 1 \right)\]
As we can see the form of the above equation is parabola means it’s in the form of the standard formula that is \[y=a{{\left( x-h \right)}^{2}}+k\].
To determine the turning point that is find \[\left( h,k \right)\], compare the given equation with the standard formula, we get that
\[\Rightarrow h=2\] and \[k=-2\]
With this we can interpret that the graph's turning point shifts \[2\] units to the right, and \[2\]units down.
Therefore, the turning point is \[\left( 2,-2 \right)\].
The next step is to find the intercepts. Recall that to find the \[y\]-intercept by putting \[x=0\], we get:
\[\Rightarrow y=0.5{{\left( \left( 0 \right)-2 \right)}^{2}}-2\]
 Now factorise the above equation and solve for \[y\], we get:
\[\Rightarrow y=0.5{{\left( -2 \right)}^{2}}-2\]
\[\Rightarrow y=0.5\times 4-2\]
\[\Rightarrow y=2-2\]
\[\Rightarrow y=0\]
The \[y\]-intercept is at the origin, \[\left( 0,0 \right)\].
Now to find the \[x\]-intercept by put \[y=0\] in equation \[\left( 1 \right)\], we get:
\[\Rightarrow 0=0.5{{\left( x-2 \right)}^{2}}-2\]
To simplify it further factorise the above equation and solve for \[x\], we get:
\[\Rightarrow 0.5{{\left( x-2 \right)}^{2}}=2\]
\[\Rightarrow {{\left( x-2 \right)}^{2}}=\dfrac{2}{0.5}\]
\[\Rightarrow {{\left( x-2 \right)}^{2}}=4\]
\[\Rightarrow {{\left( x-2 \right)}^{2}}-4=0\]
\[\Rightarrow {{\left( x-2 \right)}^{2}}-{{2}^{2}}=0\]
Now to simplify it further apply the identity \[\left( {{a}^{2}}-{{b}^{2}} \right)=\left( a+b \right)\left( a-b \right)\] where \[a=\left( x-2 \right)\] and \[b=2\]in the above equation, we get:
\[\Rightarrow \left( \left( x-2 \right)+2 \right)\left( \left( x-2 \right)-2 \right)=0\]
\[\Rightarrow x\left( x-4 \right)=0\]
\[\Rightarrow x=0\] and \[\left( x-4 \right)=0\]
\[\Rightarrow x=0,4\]
Therefore, \[x\]-intercepts are \[\left( 0,0 \right)\]and \[\left( 4,0 \right)\].
Now as we have all the information, we can sketch the graph as shown in the figure below:

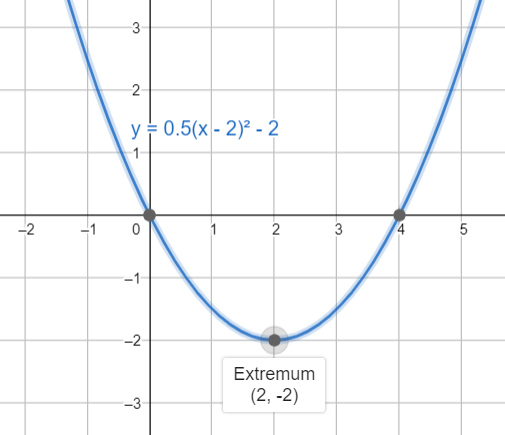
As you can see, the transformation in the above graph, that is the graph has shifted \[2\] units to the right and \[2\] units down compared to \[y={{x}^{2}}\]. The graph is also wider than \[y={{x}^{2}}\]. Since the value of \[a\] in the equation is \[\dfrac{1}{2}\].
Whereas the \[y\]-intercept is at the origin, \[\left( 0,0 \right)\]and the \[x\]-intercepts are \[\left( 0,0 \right)\]and \[\left( 4,0 \right)\].Also, The turning point is \[\left( 2,-2 \right)\].

Note: Students can go wrong while calculating the \[y\]-intercept and the \[x\]-intercepts. They make mistakes by letting \[x=0\] to find the \[x\]-intercept and let \[y=0\] to find the \[y\]-intercept which is completely wrong and further leads to the no answer. It’s important to remember to find the \[y\]-intercept, put \[x=0\]and solve for \[y\]. To find the \[x\]-intercept, put \[y=0\] and solve for \[x\].