
How do you sketch the graph of $ y = \dfrac{1}{2}{x^2} $ and describe the transformation ?
Answer
527.4k+ views
Hint: A graph of a function f is the set of ordered pairs; the equation of the graph is generally represented as $ y = f\left( x \right) $ , where x and $ f\left( x \right) $ are real numbers. We substitute the value of x and we determine the value of y and then we mark the points in the graph and we join the points. The graph for the function $ y = \dfrac{1}{2}{x^2} $ can be plotted by using the graphical transformations.
Complete step by step solution:
Here, in the given question, we have to plot the graph for the given function. A graph of a function is a set of ordered pairs and it is represented as $ y = f\left( x \right) $ , where x and $ f\left( x \right) $ are real numbers. These pairs are in the cartesian form and the graph is the two-dimensional graph.
First, we have to find the value of y by using the graph equation $ y = \dfrac{1}{2}{x^2} $ .
Let us substitute the value of x as $ 2 $ .
$ \Rightarrow y = \dfrac{1}{2}{\left( 2 \right)^2} $
$ \Rightarrow y = \dfrac{1}{2}\left( 4 \right) $
$ \Rightarrow y = 2 $
Now we consider the value of x as $ 4 $ , the value of y is
$ \Rightarrow y = \dfrac{1}{2}{\left( 4 \right)^2} $
$ \Rightarrow y = \dfrac{1}{2}\left( {16} \right) $
$ \Rightarrow y = 8 $
Now we consider the value of x as $ 3 $ , the value of y is
$ \Rightarrow y = \dfrac{1}{2}{\left( 3 \right)^2} $
$ \Rightarrow y = \dfrac{1}{2}\left( 9 \right) $
$ \Rightarrow y = 4.5 $
Now we draw a table for these values we have
We, also know the nature of the graph of square function. Hence, we can now plot the graph of the given function $ y = \dfrac{1}{2}{x^2} $ . The graph of the function $ y = \dfrac{1}{2}{x^2} $ can also be plotted using the graphical transformation. We know that the graph of $ y = {x^2} $ represents a parabola facing upwards.
So, $ y = \dfrac{1}{2}{x^2} $ also represents a parabola facing upwards with a slight vertical compression. So, in comparison to the parent function $ y = {x^2} $ , there is a vertical compression in the graph of $ y = \dfrac{1}{2}{x^2} $ .
The graph plotted for these points is represented below:
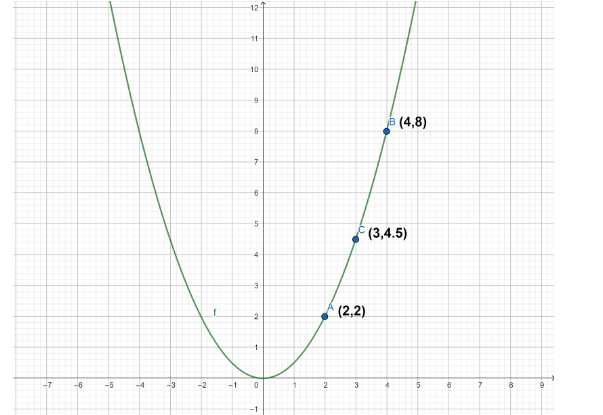
Note: The graphical transformations of the functions help us to easily plot graphs of complex and derived functions using the nature of the graphs of parent functions. Functions are plotted with the help of coordinates of the points lying on it.
Complete step by step solution:
Here, in the given question, we have to plot the graph for the given function. A graph of a function is a set of ordered pairs and it is represented as $ y = f\left( x \right) $ , where x and $ f\left( x \right) $ are real numbers. These pairs are in the cartesian form and the graph is the two-dimensional graph.
First, we have to find the value of y by using the graph equation $ y = \dfrac{1}{2}{x^2} $ .
Let us substitute the value of x as $ 2 $ .
$ \Rightarrow y = \dfrac{1}{2}{\left( 2 \right)^2} $
$ \Rightarrow y = \dfrac{1}{2}\left( 4 \right) $
$ \Rightarrow y = 2 $
Now we consider the value of x as $ 4 $ , the value of y is
$ \Rightarrow y = \dfrac{1}{2}{\left( 4 \right)^2} $
$ \Rightarrow y = \dfrac{1}{2}\left( {16} \right) $
$ \Rightarrow y = 8 $
Now we consider the value of x as $ 3 $ , the value of y is
$ \Rightarrow y = \dfrac{1}{2}{\left( 3 \right)^2} $
$ \Rightarrow y = \dfrac{1}{2}\left( 9 \right) $
$ \Rightarrow y = 4.5 $
Now we draw a table for these values we have
| x | $ 2 $ | $ 4 $ | $ 3 $ |
| y | $ 2 $ | $ 8 $ | $ 4.5 $ |
We, also know the nature of the graph of square function. Hence, we can now plot the graph of the given function $ y = \dfrac{1}{2}{x^2} $ . The graph of the function $ y = \dfrac{1}{2}{x^2} $ can also be plotted using the graphical transformation. We know that the graph of $ y = {x^2} $ represents a parabola facing upwards.
So, $ y = \dfrac{1}{2}{x^2} $ also represents a parabola facing upwards with a slight vertical compression. So, in comparison to the parent function $ y = {x^2} $ , there is a vertical compression in the graph of $ y = \dfrac{1}{2}{x^2} $ .
The graph plotted for these points is represented below:

Note: The graphical transformations of the functions help us to easily plot graphs of complex and derived functions using the nature of the graphs of parent functions. Functions are plotted with the help of coordinates of the points lying on it.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




