Question

How do you sketch the general shape of $f\left( x \right)=-{{x}^{3}}-6{{x}^{2}}-9x-4$ using end behavior?

Answer 1

Hint: Now we are given with a polynomial in x $f\left( x \right)=-{{x}^{3}}-6{{x}^{2}}-9x-4$ to solve the function we will first check the value at endpoints. Hence we will check the nature of the graph as $x\to -\infty $ and as $x\to \infty $ . Now we know that since the function is cubic it will have two extrema. One maxima and one minima. Hence we can draw the graph of the function.

Complete step by step solution:
Now we are given with a polynomial in x.
Now we know that degree of a polynomial is the highest power of the variable in the expression.
Here the highest power is three and hence the degree of the polynomial is 3.
Now polynomial with degree 3 is called cubic polynomial
Now we know by fundamental theorem of algebra that if the degree of polynomial is n then the polynomial has n roots.
Hence the given equation has 3 roots.
Now first let us check the value of the function at left extreme.
Now $x\to -\infty $ we get $f\left( x \right)\to \infty $
Now if we have $x\to \infty $ then we get $f\left( x \right)\to -\infty $
Hence the function is positive at negative extreme of x axis and negative at positive extreme of x axis.
Now since the equation has three roots it will change the sign of slope three times and hence will have two extrema.
Hence the function is first negative then reaches a local minima and changes to positive function. Then the function again changes to negative after reaching a local maxima.
Hence the general structure of graph will look like,

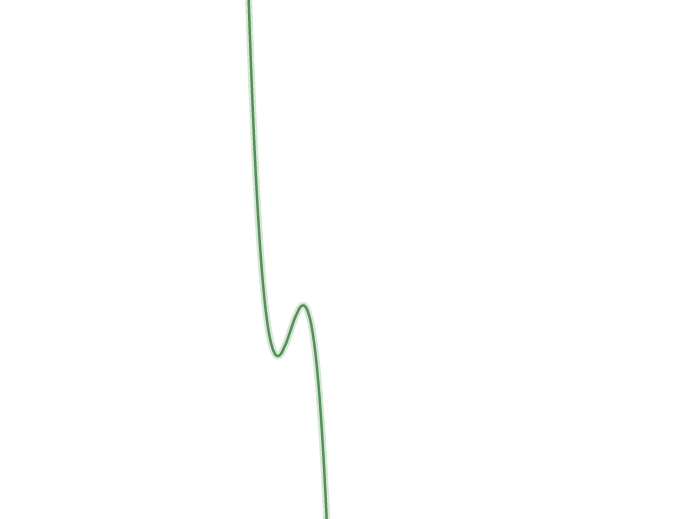
Hence we have the general structure of the graph.

Note: Now note that we have the function has three roots. It does not mean necessarily that the function cuts x axis 3 times as there is a possibility of complex roots or repeating roots. If we want to find the roots of the graph and draw a more precise graph we can factorize the equation and then find the roots.