Question

How do you sketch the curve \[y = {x^3} - 3{x^2} - 9x + 5\] by finding local maximum, minimum, inflection points, asymptotes, and intercepts?

Answer 1

Hint: In the above question, we are given a function of third order as \[y = {x^3} - 3{x^2} - 9x + 5\] . We have to find its local maximum, minimum, inflection points, asymptotes, and intercepts. First we have to find the first and second derivative to check for inflection points and the local minima and maxima. Intercepts can be found by putting \[x\] and \[f\left( x \right)\] equal to zero simultaneously. Asymptotes of a function \[f\left( x \right)\] exist only in a special case. A function \[f\left( x \right)\] will have the horizontal asymptote \[y = l\] if either \[\mathop {\lim }\limits_{x \to \infty } f\left( x \right) = l\] or \[\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = l\] . Therefore, to find the horizontal asymptotes, we simply evaluate the limit of the function as it approaches infinity, and again as it approaches negative infinity.

Complete step-by-step answer:
Given function is
\[ \Rightarrow y = {x^3} - 3{x^2} - 9x + 5\]
Differentiating once,
\[ \Rightarrow y' = 3{x^2} - 6x - 9\]
Or,
\[ \Rightarrow y' = 3\left( {x + 1} \right)\left( {x - 3} \right)\]
Differentiating again,
\[ \Rightarrow y'' = 6\left( {x - 1} \right)\]
Clearly \[y' = 0\] if \[x = - 1,3\]
Now, and
Hence, \[x = - 1,3\] are not inflections points but also the points of local maxima and local minima respectively.
Now local maxima and minima can be given as,
\[ \Rightarrow {y_{x = - 1}} = {x^3} - 3{x^2} - 9x + 5\]
That gives,
\[ \Rightarrow {y_{x = - 1}} = {\left( { - 1} \right)^3} - 3{\left( { - 1} \right)^2} - 9\left( { - 1} \right) + 5\]
Or,
\[ \Rightarrow {y_{x = - 1}} = 10\]
Similarly,
\[ \Rightarrow {y_{x = 3}} = {x^3} - 3{x^2} - 9x + 5\]
That gives,
\[ \Rightarrow {y_{x = 3}} = {\left( 3 \right)^3} - 3{\left( 3 \right)^2} - 9\left( 3 \right) + 5\]
Or,
\[ \Rightarrow {y_{x = 3}} = - 22\]
Also we can notice the limit of the function at infinity, that is
\[ \Rightarrow \mathop {\lim }\limits_{x \to \infty } y = \infty \]
And
\[ \Rightarrow \mathop {\lim }\limits_{x \to - \infty } y = - \infty \]
Therefore asymptotes for the function do not exist.
Also, now we can say that the function \[y = {x^3} - 3{x^2} - 9x + 5\] starts from \[ - \infty \] , increases till \[x = - 1\] and decreases between \[\left( { - 1,3} \right)\] and then again increases till infinity.
Therefore, the graph of the function can be plotted as shown below.

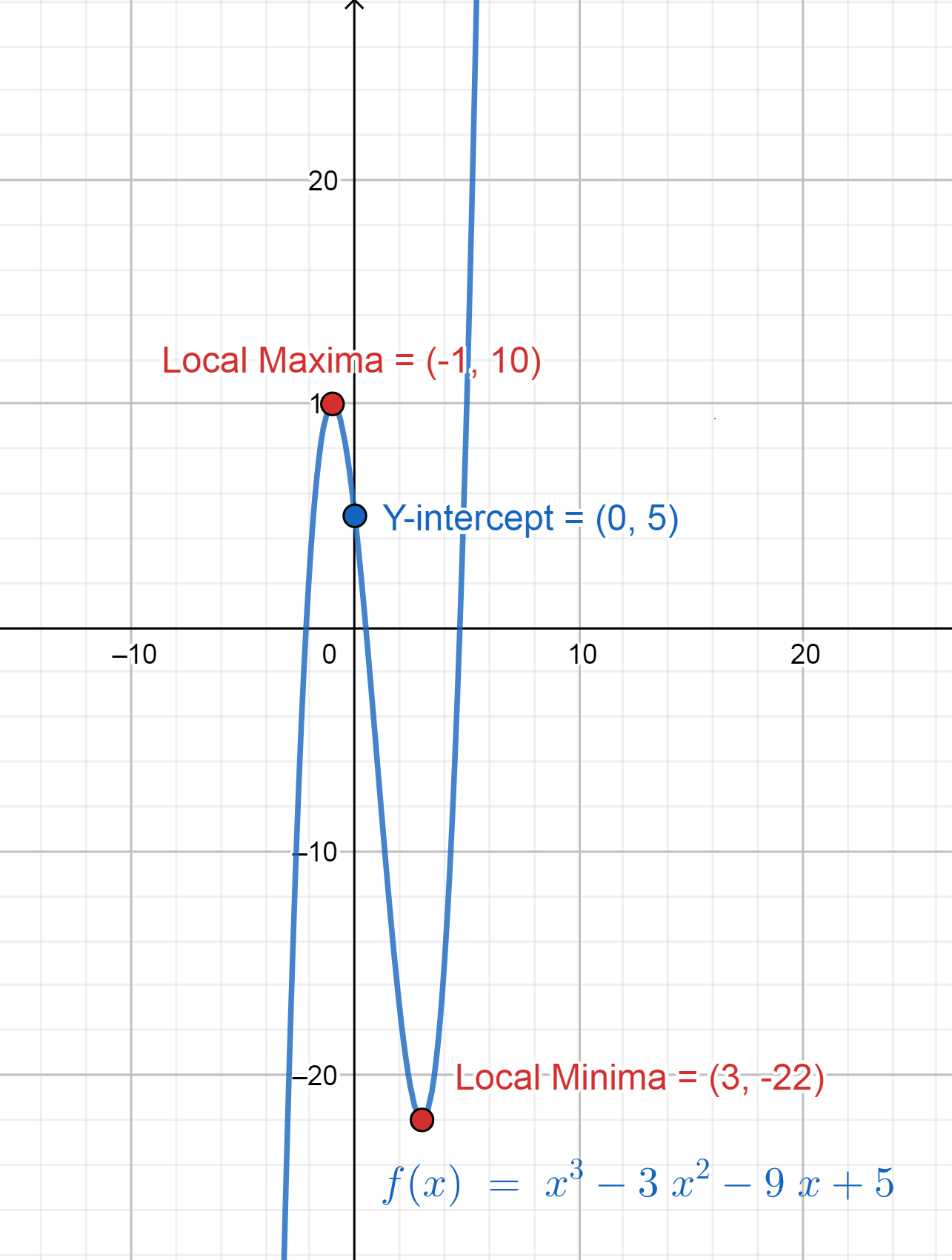
Note: Since the graph of \[y = {x^3} - 3{x^2} - 9x + 5\] is intersecting the x-axis at three different points, therefore it clarifies that the function has 3 real and distinct roots. Also the order of function is 3 that also means that it has 3 solutions. These intersections are called x-intercepts. Similarly, the curve is crossing the y-axis at the y-intercept that is \[\left( {0,5} \right)\] .