Question

Sketch the angle in standard position $ \dfrac{{ - 23\pi }}{3} $ .

Answer 1

Hint: In this problem, we have given a value of angle in radians and we have to sketch the angle given in standard position and we know that in angles, the angle starts from 0 and $ \pi = 180^\circ $ and there are four quadrants where an angle is formed. If the angle is formed from initial side rotating in counter clockwise then the measure of the angle is positive and if the angle is formed from initial side rotating in clockwise then the measure of the angle is negative.

Complete step-by-step answer:
In this problem we have to sketch an angle whose measure is negative, so, we have to rotate clockwise to form the angle. We know that, one whole round is of $ 360^\circ $ or we can say, it is of $ 2\pi $ , so a half round is of $ \pi $ .

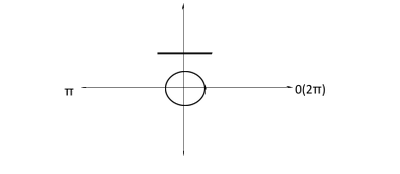
Now, we will convert the given angle in mixed fraction, $ - \dfrac{{23\pi }}{3} = - 7\dfrac{{2\pi }}{3} $ , from this we have $ 7\pi $ , now, firstly we will move upto $ 7\pi $ and then, make an angle for $ \dfrac{{2\pi }}{3} $ . We know that, one half round is $ \pi $ and now we have to complete $ 7\pi $ .

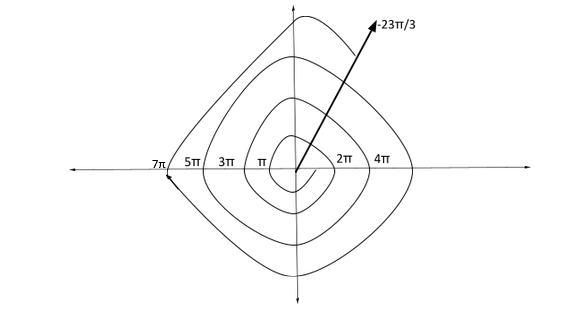
Now, we have to make an angle of $ \dfrac{{2\pi }}{3} $ from $ 7\pi $ and when we convert $ \dfrac{{2\pi }}{3} $ into degrees, we get,
 $ \dfrac{{2 \times 180}}{3} = 120^\circ $ and now, we have to make an angle of $ 120^\circ $ from $ 7\pi $ and we know that one-fourth round is of $ 90^\circ $ , after forming an angle of $ 90^\circ $ from $ 7\pi $ , we have to make an angle of $ 30^\circ $ ,as, $ 90 + 30 = 120^\circ $ . Now, we have sketched an angle in standard position.

Note: When an angle is formed there are two sides, one is initial side, from the where the angle formation starts and the other one is terminal side, which can be reached from the initial side with a rotation and when an angle with a measure is formed then that position is termed as standard position of an angle.