
How do you sketch one cycle of \[y = \sec \left( {2x} \right)?\]
Answer
556.2k+ views
Hint:We need to know the trigonometric table value for \[\cos \theta \]and\[\sec \theta \]. Also, we need to know the relation between \[\cos \theta \] and \[\sec \theta \]. Also, this question involves the operation of addition/ subtraction/ multiplication/ division. Also, we need to know how to assume the \[x\] value, by using the assumed \[x\] value we can set \[y\] the value. We need to know how to sketch graphs by using the \[x\] and \[y\] values.
Complete step by step solution:
The given equation is shown below,
\[y = \sec \left( {2x} \right) \to \left( 1 \right)\]
We know that,
\[\cos \theta = \dfrac{1}{{\sec \theta }}\]
So, first, we would find the value for \[\cos \theta \], next, we can easily find the values for \[\sec \theta \].
We get,
\[\cos 2x = \dfrac{1}{{\sec 2x}}\]
\[\sec 2x = \dfrac{1}{{\cos 2x}} \to \left( 2 \right)\]
We assume,
\[x = ....\dfrac{{ - \pi }}{2},0,\dfrac{\pi }{2},\pi ,\dfrac{{3\pi }}{2},2\pi ,.....\]
Let substitute \[x = \dfrac{{ - \pi }}{2}\] in the equation \[\left( 2 \right)\], we get
\[\left( 2 \right) \to \sec 2x = \dfrac{1}{{\cos 2x}}\]
\[
\sec \left( {2 \times \dfrac{{ - \pi }}{2}} \right) = \dfrac{1}{{\cos \left( {2 \times \dfrac{{ - \pi }}{2}}
\right)}} = \dfrac{1}{{\cos \left( { - \pi } \right)}} = \dfrac{1}{1} \\
\sec \left( {2 \times \dfrac{{ - \pi }}{2}} \right) = 1 \\
\]
Let substitute \[x = 0\]in the equation \[\left( 2 \right)\], we get
\[\left( 2 \right) \to \sec 2x = \dfrac{1}{{\cos 2x}}\]
\[
\sec \left( {2 \times 0} \right) = \dfrac{1}{{\cos \left( {2 \times 0} \right)}} = \dfrac{1}{{\cos 0}} =
\dfrac{1}{1} \\
\sec \left( {2 \times 0} \right) = 1 \\
\]
Let’s substitute\[x = \dfrac{\pi }{2}\]in the equation\[\left( 2 \right)\], we get
\[\left( 2 \right) \to \sec 2x = \dfrac{1}{{\cos 2x}}\]
\[
\sec \left( {2 \times \dfrac{\pi }{2}} \right) = \dfrac{1}{{\cos \left( {2 \times \dfrac{\pi }{2}}
\right)}} = \dfrac{1}{{\cos \left( \pi \right)}} = \dfrac{1}{{ - 1}} \\
\sec \left( {2 \times \dfrac{\pi }{2}} \right) = - 1 \\
\]
Let’s substitute \[x = \pi \]in the equation\[\left( 2 \right)\], we get
\[\left( 2 \right) \to \sec 2x = \dfrac{1}{{\cos 2x}}\]
\[
\sec \left( {2 \times \pi } \right) = \dfrac{1}{{\cos \left( {2 \times \pi } \right)}} = \dfrac{1}{{\cos
2\pi }} = \dfrac{1}{1} \\
\sec \left( {2 \times \pi } \right) = 1 \\
\]
Let’s substitute \[x = \dfrac{{3\pi }}{2}\] in the equation\[\left( 2 \right)\], we get
\[\left( 2 \right) \to \sec 2x = \dfrac{1}{{\cos 2x}}\]
\[
\sec \left( {2 \times \dfrac{{3\pi }}{2}} \right) = \dfrac{1}{{\cos \left( {2 \times \dfrac{{3\pi }}{2}}
\right)}} = \dfrac{1}{{\cos \left( {3\pi } \right)}} = \dfrac{1}{{ - 1}} \\
\sec \left( {2 \times \dfrac{{3\pi }}{2}} \right) = - 1 \\
\]
Let’s substitute \[x = 2\pi \] in the equation \[\left( 2 \right)\], we get
\[\left( 2 \right) \to \sec 2x = \dfrac{1}{{\cos 2x}}\]
\[
\sec \left( {2 \times 2\pi } \right) = \dfrac{1}{{\cos \left( {2 \times 2\pi } \right)}} = \dfrac{1}{{\cos
4\pi }} = \dfrac{1}{1} \\
\sec \left( {2 \times 2\pi } \right) = 1 \\
\]
By using these values we can make the following tabular column,
By using this tabular column we can easily make the following graph,
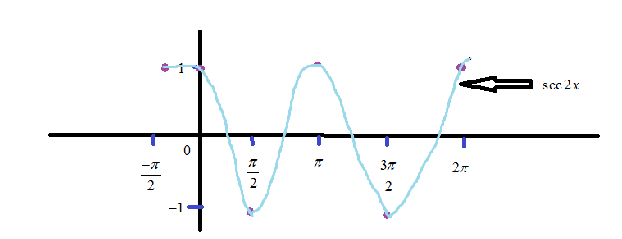
The above graph shows the one cycle of \[\sec 2x\]
Note: Note that when \[\theta \] is the end with \[\dfrac{\pi }{2}\] the term, all \[\cos \theta \] value becomes zero. Also, note that when \[\theta \] has an odd \[\pi \] term, all the \[\cos \theta \] values become \[ - 1\] and when \[\theta \] has an even \[\pi \] term, all the \[\cos \theta \] values become \[1\]. Note that when the denominator value becomes zero, then the answer becomes undefined. This question involves the operation of addition / subtraction/ multiplication/ division. Also, note that \[\cos \theta \] is the inverse value of \[\sec \theta \]. Remember the trigonometric table values to make easy calculations.
Complete step by step solution:
The given equation is shown below,
\[y = \sec \left( {2x} \right) \to \left( 1 \right)\]
We know that,
\[\cos \theta = \dfrac{1}{{\sec \theta }}\]
So, first, we would find the value for \[\cos \theta \], next, we can easily find the values for \[\sec \theta \].
We get,
\[\cos 2x = \dfrac{1}{{\sec 2x}}\]
\[\sec 2x = \dfrac{1}{{\cos 2x}} \to \left( 2 \right)\]
We assume,
\[x = ....\dfrac{{ - \pi }}{2},0,\dfrac{\pi }{2},\pi ,\dfrac{{3\pi }}{2},2\pi ,.....\]
Let substitute \[x = \dfrac{{ - \pi }}{2}\] in the equation \[\left( 2 \right)\], we get
\[\left( 2 \right) \to \sec 2x = \dfrac{1}{{\cos 2x}}\]
\[
\sec \left( {2 \times \dfrac{{ - \pi }}{2}} \right) = \dfrac{1}{{\cos \left( {2 \times \dfrac{{ - \pi }}{2}}
\right)}} = \dfrac{1}{{\cos \left( { - \pi } \right)}} = \dfrac{1}{1} \\
\sec \left( {2 \times \dfrac{{ - \pi }}{2}} \right) = 1 \\
\]
Let substitute \[x = 0\]in the equation \[\left( 2 \right)\], we get
\[\left( 2 \right) \to \sec 2x = \dfrac{1}{{\cos 2x}}\]
\[
\sec \left( {2 \times 0} \right) = \dfrac{1}{{\cos \left( {2 \times 0} \right)}} = \dfrac{1}{{\cos 0}} =
\dfrac{1}{1} \\
\sec \left( {2 \times 0} \right) = 1 \\
\]
Let’s substitute\[x = \dfrac{\pi }{2}\]in the equation\[\left( 2 \right)\], we get
\[\left( 2 \right) \to \sec 2x = \dfrac{1}{{\cos 2x}}\]
\[
\sec \left( {2 \times \dfrac{\pi }{2}} \right) = \dfrac{1}{{\cos \left( {2 \times \dfrac{\pi }{2}}
\right)}} = \dfrac{1}{{\cos \left( \pi \right)}} = \dfrac{1}{{ - 1}} \\
\sec \left( {2 \times \dfrac{\pi }{2}} \right) = - 1 \\
\]
Let’s substitute \[x = \pi \]in the equation\[\left( 2 \right)\], we get
\[\left( 2 \right) \to \sec 2x = \dfrac{1}{{\cos 2x}}\]
\[
\sec \left( {2 \times \pi } \right) = \dfrac{1}{{\cos \left( {2 \times \pi } \right)}} = \dfrac{1}{{\cos
2\pi }} = \dfrac{1}{1} \\
\sec \left( {2 \times \pi } \right) = 1 \\
\]
Let’s substitute \[x = \dfrac{{3\pi }}{2}\] in the equation\[\left( 2 \right)\], we get
\[\left( 2 \right) \to \sec 2x = \dfrac{1}{{\cos 2x}}\]
\[
\sec \left( {2 \times \dfrac{{3\pi }}{2}} \right) = \dfrac{1}{{\cos \left( {2 \times \dfrac{{3\pi }}{2}}
\right)}} = \dfrac{1}{{\cos \left( {3\pi } \right)}} = \dfrac{1}{{ - 1}} \\
\sec \left( {2 \times \dfrac{{3\pi }}{2}} \right) = - 1 \\
\]
Let’s substitute \[x = 2\pi \] in the equation \[\left( 2 \right)\], we get
\[\left( 2 \right) \to \sec 2x = \dfrac{1}{{\cos 2x}}\]
\[
\sec \left( {2 \times 2\pi } \right) = \dfrac{1}{{\cos \left( {2 \times 2\pi } \right)}} = \dfrac{1}{{\cos
4\pi }} = \dfrac{1}{1} \\
\sec \left( {2 \times 2\pi } \right) = 1 \\
\]
By using these values we can make the following tabular column,
| \[x\] | \[\dfrac{{- \pi}}{2}\] | \[0\] | \[\dfrac{\pi}{2}\] | \[\pi \] | \[\dfrac{{3\pi}}{2}\] | \[2\pi \] |
| \[y =\sec2x\] | \[1\] | \[1\] | \[ - 1\] | \[1\] | \[ - 1\] | \[1\] |
By using this tabular column we can easily make the following graph,

The above graph shows the one cycle of \[\sec 2x\]
Note: Note that when \[\theta \] is the end with \[\dfrac{\pi }{2}\] the term, all \[\cos \theta \] value becomes zero. Also, note that when \[\theta \] has an odd \[\pi \] term, all the \[\cos \theta \] values become \[ - 1\] and when \[\theta \] has an even \[\pi \] term, all the \[\cos \theta \] values become \[1\]. Note that when the denominator value becomes zero, then the answer becomes undefined. This question involves the operation of addition / subtraction/ multiplication/ division. Also, note that \[\cos \theta \] is the inverse value of \[\sec \theta \]. Remember the trigonometric table values to make easy calculations.
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE

10 examples of friction in our daily life




