Question

What is \[sin(x) + \cos(x)\] in terms of sine?

Answer 1

Hint: In this question, we need to convert \[\sin(x) + \cos(x)\] in the terms of sine. To convert \[\sin(x) + \cos(x)\] in the terms of sine expression , we will use the Trigonometric identities and functions. We can convert the given expression in two methods . One by using Pythagorean identity and also by using complement / cofunction identity ,we can easily convert the given expression in the terms of sine.
Pythagorean identity :
Mathematically , there are three Pythagorean identities. Pythagorean identities are nothing but it shows a relationship between Pythagoras theorem and trigonometric identities. If we consider a unit circle, a unit circle is a circle with radius \[1\] .
Pythagoras theorem :
Pythagoras theorem states that in a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Complete step-by-step solution:
In a right angle triangle \[ABC\] ,

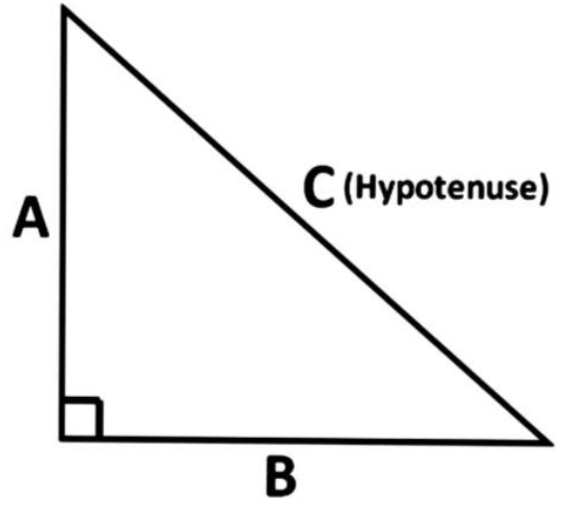
Where \[C\] is the hypotenuse, \[B\] is the base and \[A\] is the perpendicular.
According to Pythagoras theorem,
\[\text{Hypotenuse}^{2} = \text{perpendicular}^{2} + \text{base}^{2}\]
⇒ \[C^{2} = A^{2} + B^{2}\]
We are going to use one of the Pythagorean identities in this problem.
That is \[sin^{2}\theta\ + \ cos^{2}\theta\ = \ 1\]
Where \[\theta\] is the angle,
\[\sin\theta\] is the opposite side,
\[\cos\theta\] is the adjacent side,
\[1\] is the hypotenuse . With the help of the Pythagoras theorem we get this Pythagorean identity.
Here we need to convert \[\sin(x) + \cos(x)\] in the terms of sine.
Let us start with the Trigonometric identity,
\[\sin^{2}\theta\ + \cos^{2}\theta\ = \ 1\]
By keeping\[cos^{2}\theta\] one side and taking \[\sin^{2}\theta\] term to other side,
We get,
\[ \cos^{2}\theta = 1 –\sin^{2}\theta\]
On taking square root on both sides,
We get,
\[\cos\theta\ = \pm \sqrt{1 – \sin^{2}\theta}\]
By replacing \[x\] in the place of \[\theta\] ,
We get,
\[\cos x = \pm \sqrt{1 – \sin^{2}x}\]
Thus by substituting in the given expression,
Given,
\[\Rightarrow \sin(x) + \cos(x)\]
By substituting \[\cos x = \pm \sqrt{1 - \sin^{2}x}\]
We get,
\[\Rightarrow \sin x \pm \sqrt{1 - \sin^{2}x}\]
Thus we get \[\sin(x) +\cos(x)\] in the terms of sine.
That is
\[\Rightarrow \sin \left( x \right) + \cos\left( x \right) = \sin x \pm \sqrt{1 – \sin^{2}x}\]
Final answer :
\[\sin\left( x \right) + \cos\left( x \right) = \sin x\ \pm \sqrt{1 – \sin^{2}x}\]

Note: The concept used to solve the given problem is trigonometric identities and ratios. Trigonometric identities are nothing but they involve trigonometric functions including variables and constants. The common technique used in this problem is the Pythagoras theorem with the use of trigonometric functions.
Alternative solution :
We can also solve this problem by using complement / cofunction identity. Cofunction identity is nothing but it shows the relationship between all the trigonometric identities. Complement is defined as the sum of two angles is \[90^{o}\].
By using complement / cofunction identity,
Sine and cosines are co function and complement to each other.
We can write \[{cosx}\] as \[\sin\left( \dfrac{\pi}{2} – x \right)\]
Thus we get,
\[\sin\left( x \right) + cos\left( x \right) = \sin x\ +\sin\left( \dfrac{\pi}{2} – x \right)\]