Question

What is the sine, cosine and tangent of 270 degrees?

Answer 1

Hint: Express ${{270}^{\circ }}\text{ into }\left( {{270}^{\circ }}+\theta \right)$ . Then we should use the following two identities for sin and cosine respectively, $\sin \left( {{270}^{\circ }}+\theta \right)=-\cos \theta \text{ and }\cos \left( {{270}^{\circ }}+\theta \right)=\sin \theta $ . To find the tangent, we must remember that $\tan \theta =\dfrac{\sin \theta }{\cos \theta }$ . In case the value of tangent is undefined, verify using the graph of $y=\tan \theta \text{ at }\theta ={{270}^{\circ }}$ to check whether it is $+\infty \text{ or }-\infty $ .

Complete step by step solution:
For sine of 270 degrees:
We can write ${{270}^{\circ }}\text{ as }\left( {{270}^{\circ }}+{{0}^{\circ }} \right)$ . Or, in equation form
$\sin \left( {{270}^{\circ }} \right)=\sin \left( {{270}^{\circ }}+{{0}^{\circ }} \right)...\left( i \right)$
We know the trigonometric identity $\sin \left( {{270}^{\circ }}+\theta \right)=-\cos \theta $.
If we put $\theta ={{0}^{\circ }}$ and keep in mind the fact that $\cos {{0}^{\circ }}=1$ , we get
$\sin \left( {{270}^{\circ }}+{{0}^{\circ }} \right)=-\cos {{0}^{\circ }}=-1...\left( ii \right)$
Now substituting the value of $\sin \left( {{270}^{\circ }}+{{0}^{\circ }} \right)$ in equation (i), we get
$\sin \left( {{270}^{\circ }} \right)=-1$
Hence, the sine of 270 degrees is -1.

For cosine of 270 degrees:
We can write ${{270}^{\circ }}\text{ as }\left( {{270}^{\circ }}+{{0}^{\circ }} \right)$ . Or, in equation form
$\cos \left( {{270}^{\circ }} \right)=\cos \left( {{270}^{\circ }}+{{0}^{\circ }} \right)...\left( iii \right)$
We know the trigonometric identity $\cos \left( {{270}^{\circ }}+\theta \right)=\sin \theta $.
If we put $\theta ={{0}^{\circ }}$ and keep in mind the fact that $\sin {{0}^{\circ }}=0$ , we get
$\cos \left( {{270}^{\circ }}+{{0}^{\circ }} \right)=\sin {{0}^{\circ }}=0...\left( iv \right)$
Now substituting the value of $\cos \left( {{270}^{\circ }}+{{0}^{\circ }} \right)$ in equation (iii), we get
$\cos \left( {{270}^{\circ }} \right)=0$
Hence, the cosine of 270 degrees is 0.

For tangent of 270 degrees:
We are well aware of the identity that
$\tan \theta =\dfrac{\sin \theta }{\cos \theta }$
Thus, we can write
$\tan {{270}^{\circ }}=\dfrac{\sin {{270}^{\circ }}}{\cos {{270}^{\circ }}}$
We can write ${{270}^{\circ }}\text{ as }\left( {{270}^{\circ }}+{{0}^{\circ }} \right)$ . Or, in equation form
$\tan \left( {{270}^{\circ }}+{{0}^{\circ }} \right)=\dfrac{\sin \left( {{270}^{\circ }}+{{0}^{\circ }} \right)}{\cos \left( {{270}^{\circ }}+{{0}^{\circ }} \right)}$
We can now substitute the values of $\sin \left( {{270}^{\circ }}+{{0}^{\circ }} \right)\text{ and }\cos \left( {{270}^{\circ }}+{{0}^{\circ }} \right)$ from equation (ii) and equation (iv) respectively. Thus, we have,
$\tan \left( {{270}^{\circ }}+{{0}^{\circ }} \right)=\dfrac{-1}{0}$ , which is N.D. or undefined.
Now, to check whether the value is $+\infty \text{ or }-\infty $ , we should use the graph of $y=\tan \left( x \right)\text{ at }x={{270}^{\circ }}$

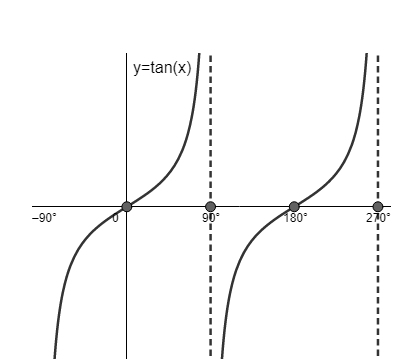
From this graph, we can clearly see that $y=\tan \left( x \right)\text{ approaches }+\infty \text{ at }x={{270}^{\circ }}$ .
\[\therefore \tan \left( {{270}^{\circ }} \right)=+\infty \]
Hence, the tangent of 270 degrees is positive infinity.

Note: We can express 270 degrees into multiple forms, such as, $\left( {{270}^{\circ }}+{{0}^{\circ }} \right),\left( {{180}^{\circ }}+{{90}^{\circ }} \right)\text{ or }\left( {{360}^{\circ }}-{{90}^{\circ }} \right)$ . All of these forms could be used separately to find the trigonometric values of ${{270}^{\circ }}$ . We should remember not to assume $\left( \dfrac{-1}{0} \right)\text{ as -}\infty $ when we are trying to find the tangent of ${{270}^{\circ }}$.