Question

What is $\sin \left( \dfrac{\theta }{2} \right)$ in terms of trigonometric functions of a unit $\theta $?

Answer 1

Hint: We first draw a right-angle triangle. We use the concept of trigonometry to find the value as $\cos \theta =\dfrac{AB}{BC}$. We use the formula of $\cos \theta =1-2{{\sin }^{2}}\left( \dfrac{\theta }{2} \right)$ to simplify the problem.
We put the values to find the solution with respect to the value of $\cos \theta =m$.

Complete step-by-step solution:
The expression of $\sin \left( \dfrac{\theta }{2} \right)$ is the formula of submultiple angles.
We have to explain the significance of the trigonometric values.
Let us assume for $\Delta ABC$, $\angle A={{90}^{\circ }}$.

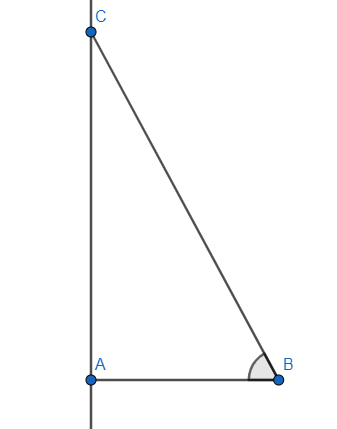
Now let us take $\angle B=\theta $.
We know the trigonometric ratio of cos gives the ratio of base and the hypotenuse.
Therefore, $\cos \theta =\dfrac{AB}{BC}$.
We will use the concept of submultiple to find the value of $\sin \left( \dfrac{\theta }{2} \right)$.
We have the relation between $\sin \left( \dfrac{\theta }{2} \right)$ and $\cos \theta $ which gives $\cos \theta =1-2{{\sin }^{2}}\left( \dfrac{\theta }{2} \right)$.
Let us assume that $\cos \theta =m$.
We get $1-2{{\sin }^{2}}\left( \dfrac{\theta }{2} \right)=m$.
From the relation we find the value of $\sin \left( \dfrac{\theta }{2} \right)$.
We get $2{{\sin }^{2}}\left( \dfrac{\theta }{2} \right)=1-m$ which gives
$\begin{align}
  & 2{{\sin }^{2}}\left( \dfrac{\theta }{2} \right)=1-m \\
 & \Rightarrow {{\left[ \sin \left( \dfrac{\theta }{2} \right) \right]}^{2}}=\dfrac{1-m}{2} \\
\end{align}$
Now we omit the root square part to find the value of $\sin \left( \dfrac{\theta }{2} \right)$.
So, ${{\left[ \sin \left( \dfrac{\theta }{2} \right) \right]}^{2}}=\dfrac{1-m}{2}\Rightarrow \sin \left( \dfrac{\theta }{2} \right)=\pm \sqrt{\dfrac{1-m}{2}}$.
The value of the trigonometric function $\sin \left( \dfrac{\theta }{2} \right)$ is $\pm \sqrt{\dfrac{1-m}{2}}$ where $\cos \theta =m$.

Note: We first need to find the relation where we have all the variables given. The use of the relation $\sin \theta =2\sin \left( \dfrac{\theta }{2} \right)\cos \left( \dfrac{\theta }{2} \right)$ also gives the same result. In this case we find two ratio values to get to the required solution.