Question

How do you simplify the square root \[ \pm \sqrt {0.64} \]

Answer 1

Hint: The square and square root are inverse to each other. Here in this we have a symbol \[\sqrt {} \], this symbol represents the square root. Here we have to find the square root of 0.64. So first we simplify the number 0.64 by using the factorisation and then we simplify the number \[ \pm \sqrt {0.64} \].

Complete step-by-step solution:
In the question we can see the\[\sqrt {} \] symbol. This symbol represents the square root. A square root is defined as a number which produces a specified quantity when multiplied by itself. The number which is in the square root is 0.64. The number is in the form of decimal. So we write the decimal with the place value and then find the square. The perfect square is defined as the number expressed as the square of a number. Since the number 75 is not a perfect square we factorise the number 75.
Now consider the number 0.64
Multiply and divide the number by 100 we have
\[ \Rightarrow 0.64 \times \dfrac{{100}}{{100}}\]
On simplifying we get
\[ \Rightarrow \dfrac{{64}}{{100}}\]
Let we factorise the terms both numerator and denominator we get
Factoring the numerator value

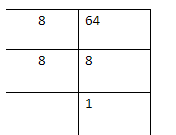
Factoring the numerator value

Therefore, the number can be written as \[64 = 8 \times 8\]. Here 8 is multiplied twice so we can write in the exponential form.
So, we have \[64 = {8^2}\]
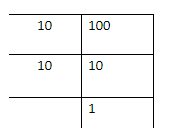
The number can be written as \[100 = 10 \times 10\]. Here 8 is multiplied twice so we can write in the exponential form.
So, we have \[100 = {10^2}\]
therefore it is written as
\[ \Rightarrow \dfrac{{64}}{{100}} = \dfrac{{{8^2}}}{{{{10}^2}}}\]
now applying the square root we have
\[ \Rightarrow \sqrt {\dfrac{{64}}{{100}}} = \sqrt {\dfrac{{{8^2}}}{{{{10}^2}}}} = \dfrac{{\sqrt {{8^2}} }}{{\sqrt {{{10}^2}} }}\]
The square and square root will get cancels and we have
\[ \Rightarrow \sqrt {\dfrac{{64}}{{100}}} = \dfrac{8}{{10}}\]
on further simplification we have
\[ \Rightarrow \sqrt {\dfrac{{64}}{{100}}} = 0.8\]
Therefore we have \[ \Rightarrow \pm \sqrt {0.64} = \pm 0.8\]

Note: When we want to find the square root of some number, let it be x. If x is a perfect square then we can obtain the result directly. Otherwise if x is not a perfect square let we factorise the x and if it possible we write the number in the form of exponential and then we simplify the number.