Question

How do you simplify the expression $\dfrac{1}{{\cos x}}?$

Answer 1

Hint: Whenever they simplify the trigonometric function, the first thing we have to do is remember the trigonometric ratios of all the functions. The given question is a direct question from the trigonometric ratios, if we know the ratios then easily we can get the answer.

Complete step-by-step answer:
Before simplifying the given expression first we should know the trigonometric ratios.
So consider the below triangle $ABC$ as shown,

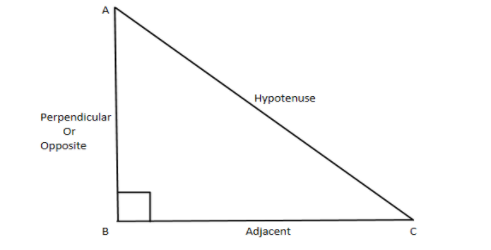
From the above diagram we have $AC = hypotenuse$ , $BC = Adjacent$ and $AB = Opposite$
So, now we can write the trigonometric ratios of functions as follows:
1: Sine function is given by: $\dfrac{{opposite}}{{hypotenuse}}$ .
2: Cosine function is given by: $\dfrac{{adjacent}}{{hypotenuse}}$.
3: Tangent function is given by: $\dfrac{{opposite}}{{adjacent}}$ .
4: Cosecant function is given by: $\dfrac{{hypotenuse}}{{opposite}}$ which is the inverse of sine function, so we can write it in terms of sine function as $\dfrac{1}{{\sin x}}$ .
5: Secant function is given by: $\dfrac{{hypotenuse}}{{adjacent}}$ which is the inverse of cosine function, so we can write it in terms of cosine function as $\dfrac{1}{{\cos x}}$ .
6: Cotangent function is given by: $\dfrac{{adjacent}}{{opposite}}$ which is the inverse of tangent function, so we can write it in terms of tangent function as $\dfrac{1}{{\tan x}}$.
Now, to simplify the given expression that is $\dfrac{1}{{\cos x}}$ refer to the above discussion.
From the above discussion it is clear that the inverse of cosine function gives us the secant function. So we can write it as:
Therefore, $\dfrac{1}{{\cos x}} = \sec x$.

Note: Whenever we have a single trigonometric function to be simplified, it can be done in single step only when we know the trigonometric ratios, so try to remember all the trigonometric ratios so that we can relate them each other and arrive at the correct answer. If we remember the ratios of sine, cosine and tangent function then you can easily remember the other three functions.