Question

How do you simplify $\tan \left( {{\sec }^{-1}}\left( u \right) \right)$ ?

Answer 1

Hint: We are given a term as $\tan \left( {{\sec }^{-1}}\left( u \right) \right)$, we have to simplify it, here simplification mean we have to write term in terms of ‘u’, to solve this we start our problem by considering ${{\sec }^{-1}}\left( u \right)$ as $\theta $ , then we will use the Pythagoras theorem we will use the ration relation with the base, perpendicular and hypotenuse, we will use that $\sec \theta =\dfrac{hypotenuse}{base}$.

Complete step by step answer:
We are given a term as $\tan \left( {{\sec }^{-1}}\left( u \right) \right)$, we have to simplify our problem means we have to solve our problem and write it in terms of ‘u’.
To do so, we start by considering ${{\sec }^{-1}}\left( u \right)$ as $\theta $ .
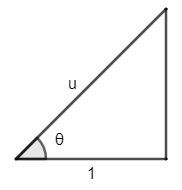
So, let ${{\sec }^{-1}}\left( u \right)=\theta $ .
By simplifying it, we get –
$u=\sec \theta $
 

Now as ‘u’ can be written as $\dfrac{u}{1}$ , so –
$\Rightarrow \sec \theta =\dfrac{u}{1}$ ……………………………… (1)
As we know that $\sec \theta $ is also given as the ratio of hypotenuse by base. So –
$\Rightarrow \sec \theta =\dfrac{hypotenuse}{base}$ ………………………. (2)
Using equation (1) and (2) we get that –
Hypotenuse = 1 and base = 1.
Now, perpendicular is not given, so we use Pythagora's theorem, which says sum of square of base and perpendicular is equal to the square of hypotenuse.
That is ${{h}^{2}}={{p}^{2}}+{{b}^{2}}$ .
As we have h=u, base =1. So we get –
$\Rightarrow {{u}^{2}}={{p}^{2}}+{{1}^{2}}$
By simplifying, we get –
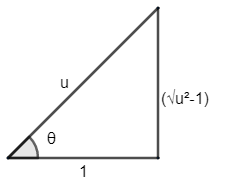
$\Rightarrow {{u}^{2}}-1={{p}^{2}}$

Solving for ‘p’, we get –
$p=\sqrt{{{u}^{2}}-1}$
Now we have $p=\sqrt{{{u}^{2}}-1}$ and base =1.
We considered ${{\sec }^{-1}}\left( u \right)$ as $\theta $ .
So, $\tan \left( {{\sec }^{-1}}\left( u \right) \right)=\tan \left( \theta \right)$ .
As we know that $\tan \theta =\dfrac{perpendicular}{base}=\dfrac{p}{b}$ .
So, we get –
$=\dfrac{p}{b}$ .
As $p=\sqrt{{{u}^{2}}-1}$ and b=1. So, we get –
$=\dfrac{\sqrt{{{u}^{2}}-1}}{1}$ .
So, we get $\tan \left( {{\sec }^{-1}}\left( u \right) \right)=\sqrt{{{u}^{2}}-1}$ .

Note:
Here we need to understand that when we solve ${{p}^{2}}={{u}^{2}}-1$ as $p=\sqrt{{{u}^{2}}-1}$ , we do not shown that ‘p’ can have $\pm \sqrt{{{u}^{2}}-1}$ , because ‘p’ is a length. So it is obvious that it will only be positive, negative value of it is never possible so we do not consider it at all.
Also we need to see that we are using correct value or not error like this may happen that we can write all given terms on one side only.
That is ${{p}^{2}}={{h}^{2}}+{{b}^{2}}$ so this will lead to the wrong answer. We need to be careful using all identities.