
Simplify: $\sqrt{18}\times \sqrt{27}\times \sqrt{128}$.
Answer
612.9k+ views
Hint: To simplify the expression given in the question, we will first prime factorise the numbers given under square root. Then we will apply rules for multiplication of irrational numbers and multiply the simplified irrational numbers to get the result.
Complete step-by-step answer:
We first need to prime factorise 18, 27 and 128.
Prime factorisation of 18,
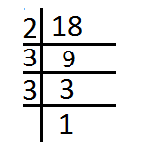
Hence,
$\begin{align}
& 18=2\times 3\times 3 \\
& \therefore \sqrt{18}=\sqrt{2\times 3\times 3} \\
& =3\sqrt{2} \\
\end{align}$
(As 3 occurs twice inside the root, so we take it one 3 outside the square root)
Prime factorisation of 27,
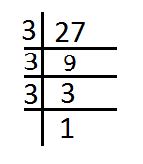
Hence,
$\begin{align}
& 27=3\times 3\times 3 \\
& \therefore \sqrt{27}=3\sqrt{3} \\
\end{align}$
Prime factorisation of 128,

Hence,
\[\begin{align}
& 128=2\times 2\times 2\times 2\times 2\times 2\times 2 \\
& \therefore \sqrt{128}=\sqrt{\underline{2\times 2}\times \underline{2\times 2}\times \underline{2\times 2}\times 2} \\
& =2\times 2\times 2\sqrt{2} \\
& =8\sqrt{2} \\
\end{align}\]
So, the expression $\sqrt{18}\times \sqrt{27}\times \sqrt{128}$ can be written as,
$\begin{align}
& \Rightarrow 3\sqrt{2}\times 3\sqrt{3}\times 8\sqrt{2} \\
& \Rightarrow \left( 3\sqrt{2}\times 8\sqrt{2} \right)\times 3\sqrt{3} \\
& \text{since, }\sqrt{2}\times \sqrt{2}=2 \\
& \text{Hence,} \\
& \left( 3\sqrt{2}\times 8\sqrt{2} \right)\times 3\sqrt{3}\Rightarrow \left( 3\times 8\times \sqrt{2}\times \sqrt{2} \right)\times 3\sqrt{3} \\
& =\left( 24\times 2 \right)\times 3\sqrt{3} \\
& =144\sqrt{3} \\
& \text{since,}\left( a\times b\sqrt{c}=ab\sqrt{c} \right) \\
\end{align}$
Therefore, $\sqrt{18}\times \sqrt{27}\times \sqrt{128}=144\sqrt{3}$.
Note: Students can also solve this question by first multiplying the numbers under the square root and then they can obtain the answer by prime factorisation the product obtained under the square root.
Method II:
$\begin{align}
& \sqrt{18}\times \sqrt{27}\times \sqrt{128} \\
& =\sqrt{18\times 27\times 128} \\
& =\sqrt{\left( 18 \right)\left( 27 \right)\left( 128 \right)} \\
& \left( \because \sqrt{a}\times \sqrt{b}\times \sqrt{c}=\sqrt{a\times b\times c}=\sqrt{abc} \right) \\
& \therefore \sqrt{18\times 27\times 128}=\sqrt{62208} \\
\end{align}$
Now, we will do prime factorisation of 62208,

Hence,
$\begin{align}
& 62208={{2}^{2}}\times {{2}^{2}}\times {{2}^{2}}\times {{2}^{2}}\times {{3}^{2}}\times {{3}^{2}}\times 3 \\
& \therefore \sqrt{62208}=2\times 2\times 2\times 2\times 3\times 3\times \sqrt{3} \\
& =144\sqrt{3} \\
\end{align}$
Therefore, $\sqrt{18}\times \sqrt{27}\times \sqrt{128}=144\sqrt{3}$.
Complete step-by-step answer:
We first need to prime factorise 18, 27 and 128.
Prime factorisation of 18,
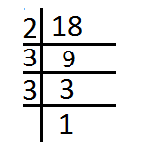
Hence,
$\begin{align}
& 18=2\times 3\times 3 \\
& \therefore \sqrt{18}=\sqrt{2\times 3\times 3} \\
& =3\sqrt{2} \\
\end{align}$
(As 3 occurs twice inside the root, so we take it one 3 outside the square root)
Prime factorisation of 27,
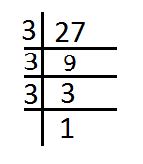
Hence,
$\begin{align}
& 27=3\times 3\times 3 \\
& \therefore \sqrt{27}=3\sqrt{3} \\
\end{align}$
Prime factorisation of 128,

Hence,
\[\begin{align}
& 128=2\times 2\times 2\times 2\times 2\times 2\times 2 \\
& \therefore \sqrt{128}=\sqrt{\underline{2\times 2}\times \underline{2\times 2}\times \underline{2\times 2}\times 2} \\
& =2\times 2\times 2\sqrt{2} \\
& =8\sqrt{2} \\
\end{align}\]
So, the expression $\sqrt{18}\times \sqrt{27}\times \sqrt{128}$ can be written as,
$\begin{align}
& \Rightarrow 3\sqrt{2}\times 3\sqrt{3}\times 8\sqrt{2} \\
& \Rightarrow \left( 3\sqrt{2}\times 8\sqrt{2} \right)\times 3\sqrt{3} \\
& \text{since, }\sqrt{2}\times \sqrt{2}=2 \\
& \text{Hence,} \\
& \left( 3\sqrt{2}\times 8\sqrt{2} \right)\times 3\sqrt{3}\Rightarrow \left( 3\times 8\times \sqrt{2}\times \sqrt{2} \right)\times 3\sqrt{3} \\
& =\left( 24\times 2 \right)\times 3\sqrt{3} \\
& =144\sqrt{3} \\
& \text{since,}\left( a\times b\sqrt{c}=ab\sqrt{c} \right) \\
\end{align}$
Therefore, $\sqrt{18}\times \sqrt{27}\times \sqrt{128}=144\sqrt{3}$.
Note: Students can also solve this question by first multiplying the numbers under the square root and then they can obtain the answer by prime factorisation the product obtained under the square root.
Method II:
$\begin{align}
& \sqrt{18}\times \sqrt{27}\times \sqrt{128} \\
& =\sqrt{18\times 27\times 128} \\
& =\sqrt{\left( 18 \right)\left( 27 \right)\left( 128 \right)} \\
& \left( \because \sqrt{a}\times \sqrt{b}\times \sqrt{c}=\sqrt{a\times b\times c}=\sqrt{abc} \right) \\
& \therefore \sqrt{18\times 27\times 128}=\sqrt{62208} \\
\end{align}$
Now, we will do prime factorisation of 62208,

Hence,
$\begin{align}
& 62208={{2}^{2}}\times {{2}^{2}}\times {{2}^{2}}\times {{2}^{2}}\times {{3}^{2}}\times {{3}^{2}}\times 3 \\
& \therefore \sqrt{62208}=2\times 2\times 2\times 2\times 3\times 3\times \sqrt{3} \\
& =144\sqrt{3} \\
\end{align}$
Therefore, $\sqrt{18}\times \sqrt{27}\times \sqrt{128}=144\sqrt{3}$.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE




