Question

How do you simplify \[\ln \left( x+3 \right)+\ln \left( x-3 \right)=\ln 16\]?

Answer 1

Hint: Apply the formula: - \[\ln m+\ln n=\ln \left( mn \right)\] in the expression present in the left-hand side. Now, compare the arguments of the logarithmic function by removing \[\ln \] from both the sides. Solve the quadratic equation obtained to obtain the values of x. Reject the value of x that is invalid by using the information that “argument of the logarithmic function must be greater than 0”.

Complete step by step answer:
Here, we have been provided with the equation: - \[\ln \left( x+3 \right)+\ln \left( x-3 \right)=\ln 16\] and we are asked to simplify it, that means we have to find the value of x.
Now, applying the sum to protect conversion formula of log given as: - \[\ln m+\ln n=\ln \left( mn \right)\], we have,
\[\Rightarrow \ln \left[ \left( x+3 \right)\left( x-3 \right) \right]=\ln 16\]
Here, ln is the natural log, i.e., log to the base \[\left( {{\log }_{e}} \right)\]. So, using the algebraic identity: - \[\left( a+b \right)\left( a-b \right)\], we get,
\[\begin{align}
  & \Rightarrow \ln \left( {{x}^{2}}-{{3}^{2}} \right)=\ln 16 \\
 & \Rightarrow \ln \left( {{x}^{2}}-9 \right)=\ln 16 \\
\end{align}\]
Now, comparing the arguments of ln on both the sides by removing the logarithmic function, we have,
\[\begin{align}
  & \Rightarrow {{x}^{2}}-9=16 \\
 & \Rightarrow {{x}^{2}}-9-16=0 \\
 & \Rightarrow {{x}^{2}}-25=0 \\
 & \Rightarrow {{x}^{2}}-{{5}^{2}}=0 \\
\end{align}\]
Again, using the algebraic identity: - \[{{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right)\], we get,
\[\Rightarrow \left( x+5 \right)\left( x-5 \right)=0\]
Substituting each term equal to 0, one – by – one, we get,
\[\Rightarrow x+5=0\] or x – 5 = 0
\[\Rightarrow x=-5\] or x = 5
Here, we have obtained two values of x. Now, let us check if any of the two values is invalid or not.
We know that a logarithmic function is only defined when its argument is greater than 0 and base is greater than 0 but unequal to 1. In the above question we have log to the base ‘e’ and the value of ‘e’ is 2.71 which is greater than 0 and also unequal to 1. So, base is defined. Now, let us define the argument. In the L.H.S. we have (x + 3) and (x – 3) as the arguments. So, we must have,
(i) x + 3 > 0 \[\Rightarrow \] x > - 3 \[\Rightarrow x\in \left( -3,\infty \right)\]
(ii) x – 3 > 0 \[\Rightarrow \] x > 3 \[\Rightarrow x\in \left( 3,\infty \right)\]
Since, we need to satisfy both the conditions, therefore we must consider the intersection of the two sets of values of x obtained. So, we have,

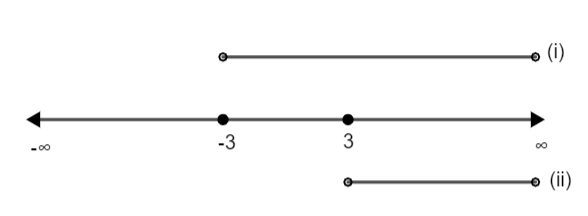
Therefore, \[x\in \left( 3,\infty \right)\], which is the final condition.
Clearly, we can see that x = -5 does not satisfy the above condition, therefore x = -5 must be rejected.

Hence, x = 5 is our answer.

Note: One may note that we cannot remove the logarithmic function directly from the initial expression: - \[\ln \left( x+3 \right)+\ln \left( x-3 \right)=\ln 16\], because it will be a wrong approach. First, we need to convert the two logarithmic terms in the L.H.S into a single logarithmic term by using the sum to product rule and then only we can remove the function. Remember that we do not just have to calculate the value of x but we must check if it satisfies the domain or not. We must reject the invalid value as it makes the function undefined.