Question

Simplify:
\[\dfrac{{{{\sin }^3}\theta + {{\cos }^3}\theta }}{{\sin \theta + \cos \theta }} + \sin \theta \cos \theta \]

Answer 1

Hint: Here we will use the formula of \[\left( {{a^3} + {b^3}} \right) = \left( {a + b} \right)\left( {{a^2} + {b^2} - ab} \right)\], \[a\] and \[b\] are two different values. We will simplify using this formula to simplify the given trigonometric equation.

Complete step-by-step solution:
Step 1: By comparing the given term \[{\sin ^3}\theta + {\cos ^3}\theta \] with the formula \[\left( {{a^3} + {b^3}} \right) = \left( {a + b} \right)\left( {{a^2} + {b^2} - ab} \right)\], we can write it as below:
\[ \Rightarrow \left( {{{\sin }^3}\theta + {{\cos }^3}\theta } \right) = \left( {\sin \theta + \cos \theta } \right)\left( {{{\sin }^2}\theta + {{\cos }^2}\theta - \sin \theta \cos \theta } \right)\]
By substituting this value in this given expression \[\dfrac{{{{\sin }^3}\theta + {{\cos }^3}\theta }}{{\sin \theta + \cos \theta }} + \sin \theta \cos \theta \] , we get:
\[ \Rightarrow \dfrac{{\left( {\sin \theta + \cos \theta } \right)\left( {{{\sin }^2}\theta + {{\cos }^2}\theta - \sin \theta \cos \theta } \right)}}{{\sin \theta + \cos \theta }} + \sin \theta \cos \theta \] ……………………… (1)
Step 2: By dividing the term \[\sin \theta + \cos \theta \] from the numerator and denominator side, we get:
\[ \Rightarrow \left( {{{\sin }^2}\theta + {{\cos }^2}\theta - \sin \theta \cos \theta } \right) + \sin \theta \cos \theta \]
By eliminating the term \[\sin \theta \cos \theta \] from the above expression \[\left( {{{\sin }^2}\theta + {{\cos }^2}\theta - \sin \theta \cos \theta } \right) + \sin \theta \cos \theta \], we get:
\[ \Rightarrow {\sin ^2}\theta + {\cos ^2}\theta \]
Step 3: As we know the value of \[{\sin ^2}\theta + {\cos ^2}\theta = 1\], so the answer will be equal to \[1\].

\[\therefore \dfrac{{{{\sin }^3}\theta + {{\cos }^3}\theta }}{{\sin \theta + \cos \theta }} + \sin \theta \cos \theta = 1\]

Note: Students need to remember the basic formulas for solving these types of questions. Some of them are mentioned below:
\[{\left( {a + b} \right)^2} = \left( {{a^2} + {b^2} + 2ab} \right)\]
\[{\left( {a - b} \right)^2} = \left( {{a^2} + {b^2} - 2ab} \right)\]
\[{\left( {a + b} \right)^3} = {a^3} + {b^3} + 3ab\left( {a + b} \right)\]
\[{\left( {a - b} \right)^3} = {a^3} - {b^3} - 3ab\left( {a - b} \right)\]
\[\left( {{a^3} + {b^3}} \right) = \left( {a + b} \right)\left( {{a^2} + {b^2} - ab} \right)\]
\[\left( {{a^3} + {b^3}} \right) = \left( {a - b} \right)\left( {{a^2} + {b^2} + ab} \right)\]
Also, students need to remember that the value of \[{\sin ^2}\theta + {\cos ^2}\theta = 1\] , proof of which as shown below for your better understanding:
Assume that in a triangle, there are three sides of length \[x\], \[y\]and \[z\] as shown in the below figure:

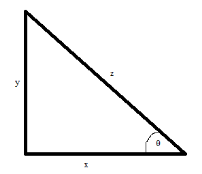
As we know
\[\sin \theta = \dfrac{y}{z}\] , i.e. the Opposite side is divided by the hypotenuses. And the \[\cos \theta = \dfrac{x}{z}\], i.e. base divided by the hypotenuses.
By using the Pythagoras theorem, we get:
\[{z^2} = {x^2} + {y^2}\] i.e. \[{\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Base}}} \right)^2} + {\left( {{\text{height}}} \right)^2}\]
Also,
\[{\sin ^2}\theta + {\cos ^2}\theta = {\left( {\dfrac{y}{z}} \right)^2} + {\left( {\dfrac{x}{z}} \right)^2}\], by taking \[z\] common from the denominator part and adding the numerator one we get: