
Simplify \[4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha )\]
A.\[\sqrt 3 - 2\sin 2\alpha \]
B. \[\sqrt 3 + 2\sin 2\alpha \]
C. \[\sqrt 3 - 2\cos 2\alpha \]
D. \[\sqrt 3 + 2\cos 2\alpha \]
Answer
589.5k+ views
Hint: We use the trigonometric formulas of \[\sin (A - B)\] and \[\cos (A + B)\] to expand the terms given in the question. Substitute the values in the expansion using a table that gives us the value of simple trigonometric functions at few angles. Multiply the expanded values according to the question and use the identity \[{\sin ^2}x + {\cos ^2}x = 1\] to solve further.
* \[\sin (A - B) = \sin A\cos B - \cos A\sin B\]
* \[\cos (A + B) = \cos A\cos B - \sin A\sin B\]
* Table for trigonometric functions like sine, cosine and tan at angles \[{0^ \circ },{30^ \circ },{45^ \circ },{60^ \circ },{90^ \circ }\] is
Complete step by step answer:
We have to find the value of \[4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha )\] ………………..… (1)
We can write \[{420^ \circ } = {360^ \circ } + {60^ \circ }\]
\[ \Rightarrow \sin ({420^ \circ } - \alpha ) = \sin ({360^ \circ } + {60^ \circ } - \alpha )\]
Group the angle in the bracket in RHS
\[ \Rightarrow \sin ({420^ \circ } - \alpha ) = \sin ({360^ \circ } + ({60^ \circ } - \alpha ))\]
We use quadrant diagram to find the value of RHS

From the quadrant diagram we know \[\sin ({360^ \circ } + x) = \sin x\]
\[ \Rightarrow \sin ({420^ \circ } - \alpha ) = \sin ({60^ \circ } - \alpha )\]
Now equation (1) becomes
\[4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = 4\sin ({60^ \circ } - \alpha )\cos ({60^ \circ } + \alpha )\] ……………….… (2)
We solve the two terms \[\sin ({60^ \circ } - \alpha )\] and \[\cos ({60^ \circ } + \alpha )\] separately.
We know \[\sin (A - B) = \sin A\cos B - \cos A\sin B\]
Substitute the value of \[A = {60^ \circ },B = \alpha \]
\[ \Rightarrow \sin ({60^ \circ } - \alpha ) = \sin {60^ \circ }\cos \alpha - \cos {60^ \circ }\sin \alpha \]
From the table of values of trigonometric terms \[\sin {60^ \circ } = \dfrac{{\sqrt 3 }}{2},\cos {60^ \circ } = \dfrac{1}{2}\]
\[ \Rightarrow \sin ({60^ \circ } - \alpha ) = \dfrac{{\sqrt 3 }}{2}\cos \alpha - \dfrac{1}{2}\sin \alpha \]
Take LCM in RHS of the equation
\[ \Rightarrow \sin ({60^ \circ } - \alpha ) = \dfrac{{\sqrt 3 \cos \alpha - \sin \alpha }}{2}\] ………….… (3)
We know \[\cos (A + B) = \cos A\cos B - \sin A\sin B\]
Substitute the value of \[A = {60^ \circ },B = \alpha \]
\[ \Rightarrow \cos ({60^ \circ } + \alpha ) = \cos {60^ \circ }\cos \alpha - \sin {60^ \circ }\sin \alpha \]
From the table of values of trigonometric terms \[\sin {60^ \circ } = \dfrac{{\sqrt 3 }}{2},\cos {60^ \circ } = \dfrac{1}{2}\]
\[ \Rightarrow \cos ({60^ \circ } + \alpha ) = \dfrac{1}{2}\cos \alpha - \dfrac{{\sqrt 3 }}{2}\sin \alpha \]
Take LCM in RHS of the equation
\[ \Rightarrow \cos ({60^ \circ } + \alpha ) = \dfrac{{\cos \alpha - \sqrt 3 \sin \alpha }}{2}\] … (4)
Substitute the values from equation (3) and (4) back in equation (2) i.e.
\[4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = 4\sin ({60^ \circ } - \alpha )\cos ({60^ \circ } + \alpha )\]
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = 4 \times \left( {\dfrac{{\sqrt 3 \cos \alpha - \sin \alpha }}{2}} \right) \times \left( {\dfrac{{\cos \alpha - \sqrt 3 \sin \alpha }}{2}} \right)\]
Cancel the same factors from numerator and denominator in RHS of the equation
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = \left( {\sqrt 3 \cos \alpha - \sin \alpha } \right)\left( {\cos \alpha - \sqrt 3 \sin \alpha } \right)\]
Multiply the brackets in RHS of the equation
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = \sqrt 3 \cos \alpha \left( {\cos \alpha - \sqrt 3 \sin \alpha } \right) - \sin \alpha \left( {\cos \alpha - \sqrt 3 \sin \alpha } \right)\]
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = \sqrt 3 \cos \alpha \times \cos \alpha - \sqrt 3 \cos \alpha \sqrt 3 \sin \alpha - \sin \alpha \cos \alpha + \sin \alpha \sqrt 3 \sin \alpha \]
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = \sqrt 3 {\cos ^2}\alpha - 3\cos \alpha \sin \alpha - \sin \alpha \cos \alpha + \sqrt 3 {\sin ^2}\alpha \]
Collect the terms having common factor between them
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = \left( {\sqrt 3 {{\cos }^2}\alpha + \sqrt 3 {{\sin }^2}\alpha } \right) + \left( { - 3\cos \alpha \sin \alpha - \cos \alpha \sin \alpha } \right)\]
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = \sqrt 3 \left( {{{\cos }^2}\alpha + {{\sin }^2}\alpha } \right) - \cos \alpha \sin \alpha \left( {3 + 1} \right)\]
Use the trigonometric identity \[{\sin ^2}x + {\cos ^2}x = 1\] in RHS of the equation
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = \sqrt 3 - 4\cos \alpha \sin \alpha \]
We can write
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = \sqrt 3 - 2(2\cos \alpha \sin \alpha )\]
We know \[2\sin x\cos x = \sin 2x\]
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = \sqrt 3 - 2\sin 2\alpha \]
\[\therefore \]Value of \[4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha )\] is \[\sqrt 3 - 2\sin 2\alpha \]
\[\therefore \] Option A is correct.
Note:
Alternate method:
Since we know the trigonometric formula \[2\sin A\cos B = \sin (A + B) + \sin (A - B)\]
We have to find the value of \[4\sin ({420^ \circ } - \alpha )\sin ({60^ \circ } + \alpha )\]
We can write
\[4\sin ({420^ \circ } - \alpha )\sin ({60^ \circ } + \alpha ) = 2\left\{ {2\sin ({{420}^ \circ } - \alpha )\sin ({{60}^ \circ } + \alpha )} \right\}\]
Apply the formula \[2\sin A\cos B = \sin (A + B) + \sin (A - B)\] in RHS of the equation
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\sin ({60^ \circ } + \alpha ) = 2\left\{ {\sin \left( {({{420}^ \circ } - \alpha ) + ({{60}^ \circ } + \alpha )} \right) + \sin \left( {({{420}^ \circ } - \alpha ) - ({{60}^ \circ } + \alpha )} \right)} \right\}\]
Calculate the angle inside the brackets in RHS
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\sin ({60^ \circ } + \alpha ) = 2\left\{ {\sin \left( {{{420}^ \circ } - \alpha + {{60}^ \circ } + \alpha } \right) + \sin \left( {{{420}^ \circ } - \alpha - {{60}^ \circ } - \alpha } \right)} \right\}\]
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\sin ({60^ \circ } + \alpha ) = 2\left\{ {\sin \left( {{{480}^ \circ }} \right) + \sin \left( {{{360}^ \circ } - 2\alpha } \right)} \right\}\] … (1)
We can write \[\sin ({480^ \circ }) = \sin ({540^ \circ } - {60^ \circ })\]
From the quadrant diagram
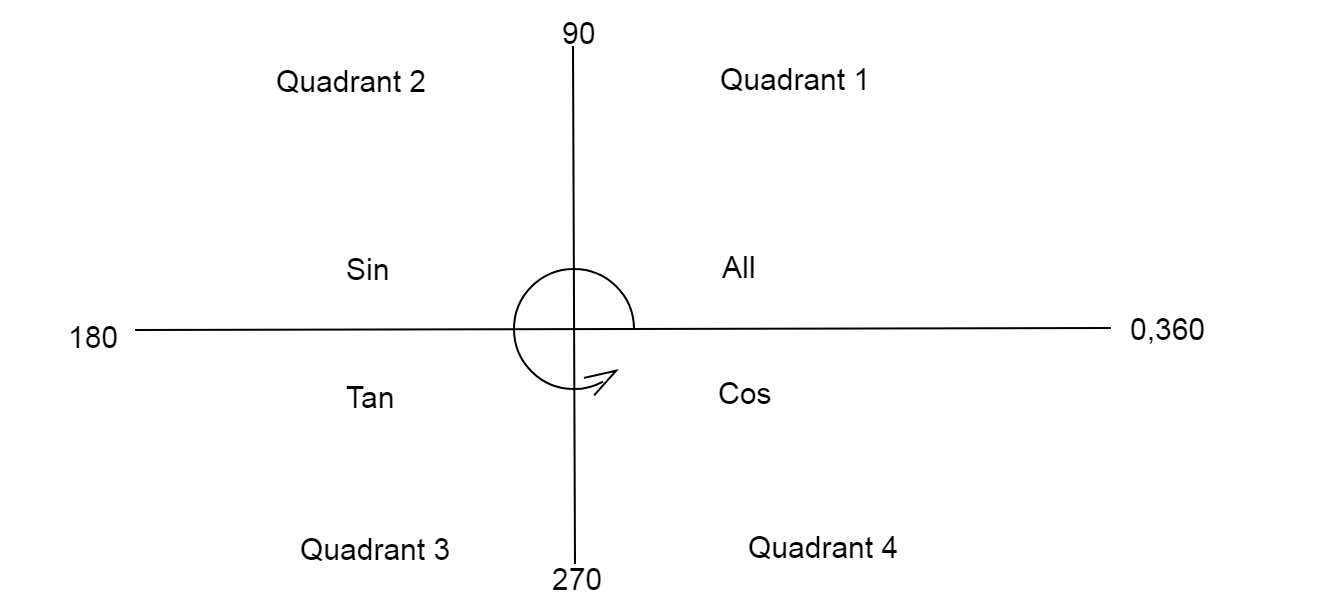
\[\sin (3\pi - x) = \sin x\]
\[ \Rightarrow \sin ({480^ \circ }) = \sin ({60^ \circ })\]
From the table we have \[\sin {60^ \circ } = \dfrac{{\sqrt 3 }}{2}\]
\[\therefore \sin ({480^ \circ }) = \dfrac{{\sqrt 3 }}{2}\]
We can write \[\sin \left( {{{360}^ \circ } - 2\alpha } \right) = - \sin 2\alpha \] because as we move in backward direction in the quadrant diagram, value of sine becomes negative
\[\therefore \sin ({360^ \circ } - 2\alpha ) = - \sin 2\alpha \]
Substitute the values in equation (1)
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = 2\left\{ {\dfrac{{\sqrt 3 }}{2} - \sin 2\alpha } \right\}\]
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = \sqrt 3 - 2\sin 2\alpha \]
\[\therefore \] Option A is correct.
* \[\sin (A - B) = \sin A\cos B - \cos A\sin B\]
* \[\cos (A + B) = \cos A\cos B - \sin A\sin B\]
* Table for trigonometric functions like sine, cosine and tan at angles \[{0^ \circ },{30^ \circ },{45^ \circ },{60^ \circ },{90^ \circ }\] is
| ANGLEFUNCTION | \[{0^ \circ }\] | \[{30^ \circ }\] | \[{45^ \circ }\] | \[{60^ \circ }\] | \[{90^ \circ }\] |
| Sin | 0 | \[\dfrac{1}{2}\] | \[\dfrac{1}{{\sqrt 2 }}\] | \[\dfrac{{\sqrt 3 }}{2}\] | 1 |
| Cos | 1 | \[\dfrac{{\sqrt 3 }}{2}\] | \[\dfrac{1}{{\sqrt 2 }}\] | \[\dfrac{1}{2}\] | 0 |
| Tan | 0 | \[\dfrac{1}{{\sqrt 3 }}\] | 1 | \[\sqrt 3 \] | Not defined |
Complete step by step answer:
We have to find the value of \[4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha )\] ………………..… (1)
We can write \[{420^ \circ } = {360^ \circ } + {60^ \circ }\]
\[ \Rightarrow \sin ({420^ \circ } - \alpha ) = \sin ({360^ \circ } + {60^ \circ } - \alpha )\]
Group the angle in the bracket in RHS
\[ \Rightarrow \sin ({420^ \circ } - \alpha ) = \sin ({360^ \circ } + ({60^ \circ } - \alpha ))\]
We use quadrant diagram to find the value of RHS

From the quadrant diagram we know \[\sin ({360^ \circ } + x) = \sin x\]
\[ \Rightarrow \sin ({420^ \circ } - \alpha ) = \sin ({60^ \circ } - \alpha )\]
Now equation (1) becomes
\[4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = 4\sin ({60^ \circ } - \alpha )\cos ({60^ \circ } + \alpha )\] ……………….… (2)
We solve the two terms \[\sin ({60^ \circ } - \alpha )\] and \[\cos ({60^ \circ } + \alpha )\] separately.
We know \[\sin (A - B) = \sin A\cos B - \cos A\sin B\]
Substitute the value of \[A = {60^ \circ },B = \alpha \]
\[ \Rightarrow \sin ({60^ \circ } - \alpha ) = \sin {60^ \circ }\cos \alpha - \cos {60^ \circ }\sin \alpha \]
From the table of values of trigonometric terms \[\sin {60^ \circ } = \dfrac{{\sqrt 3 }}{2},\cos {60^ \circ } = \dfrac{1}{2}\]
\[ \Rightarrow \sin ({60^ \circ } - \alpha ) = \dfrac{{\sqrt 3 }}{2}\cos \alpha - \dfrac{1}{2}\sin \alpha \]
Take LCM in RHS of the equation
\[ \Rightarrow \sin ({60^ \circ } - \alpha ) = \dfrac{{\sqrt 3 \cos \alpha - \sin \alpha }}{2}\] ………….… (3)
We know \[\cos (A + B) = \cos A\cos B - \sin A\sin B\]
Substitute the value of \[A = {60^ \circ },B = \alpha \]
\[ \Rightarrow \cos ({60^ \circ } + \alpha ) = \cos {60^ \circ }\cos \alpha - \sin {60^ \circ }\sin \alpha \]
From the table of values of trigonometric terms \[\sin {60^ \circ } = \dfrac{{\sqrt 3 }}{2},\cos {60^ \circ } = \dfrac{1}{2}\]
\[ \Rightarrow \cos ({60^ \circ } + \alpha ) = \dfrac{1}{2}\cos \alpha - \dfrac{{\sqrt 3 }}{2}\sin \alpha \]
Take LCM in RHS of the equation
\[ \Rightarrow \cos ({60^ \circ } + \alpha ) = \dfrac{{\cos \alpha - \sqrt 3 \sin \alpha }}{2}\] … (4)
Substitute the values from equation (3) and (4) back in equation (2) i.e.
\[4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = 4\sin ({60^ \circ } - \alpha )\cos ({60^ \circ } + \alpha )\]
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = 4 \times \left( {\dfrac{{\sqrt 3 \cos \alpha - \sin \alpha }}{2}} \right) \times \left( {\dfrac{{\cos \alpha - \sqrt 3 \sin \alpha }}{2}} \right)\]
Cancel the same factors from numerator and denominator in RHS of the equation
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = \left( {\sqrt 3 \cos \alpha - \sin \alpha } \right)\left( {\cos \alpha - \sqrt 3 \sin \alpha } \right)\]
Multiply the brackets in RHS of the equation
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = \sqrt 3 \cos \alpha \left( {\cos \alpha - \sqrt 3 \sin \alpha } \right) - \sin \alpha \left( {\cos \alpha - \sqrt 3 \sin \alpha } \right)\]
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = \sqrt 3 \cos \alpha \times \cos \alpha - \sqrt 3 \cos \alpha \sqrt 3 \sin \alpha - \sin \alpha \cos \alpha + \sin \alpha \sqrt 3 \sin \alpha \]
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = \sqrt 3 {\cos ^2}\alpha - 3\cos \alpha \sin \alpha - \sin \alpha \cos \alpha + \sqrt 3 {\sin ^2}\alpha \]
Collect the terms having common factor between them
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = \left( {\sqrt 3 {{\cos }^2}\alpha + \sqrt 3 {{\sin }^2}\alpha } \right) + \left( { - 3\cos \alpha \sin \alpha - \cos \alpha \sin \alpha } \right)\]
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = \sqrt 3 \left( {{{\cos }^2}\alpha + {{\sin }^2}\alpha } \right) - \cos \alpha \sin \alpha \left( {3 + 1} \right)\]
Use the trigonometric identity \[{\sin ^2}x + {\cos ^2}x = 1\] in RHS of the equation
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = \sqrt 3 - 4\cos \alpha \sin \alpha \]
We can write
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = \sqrt 3 - 2(2\cos \alpha \sin \alpha )\]
We know \[2\sin x\cos x = \sin 2x\]
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = \sqrt 3 - 2\sin 2\alpha \]
\[\therefore \]Value of \[4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha )\] is \[\sqrt 3 - 2\sin 2\alpha \]
\[\therefore \] Option A is correct.
Note:
Alternate method:
Since we know the trigonometric formula \[2\sin A\cos B = \sin (A + B) + \sin (A - B)\]
We have to find the value of \[4\sin ({420^ \circ } - \alpha )\sin ({60^ \circ } + \alpha )\]
We can write
\[4\sin ({420^ \circ } - \alpha )\sin ({60^ \circ } + \alpha ) = 2\left\{ {2\sin ({{420}^ \circ } - \alpha )\sin ({{60}^ \circ } + \alpha )} \right\}\]
Apply the formula \[2\sin A\cos B = \sin (A + B) + \sin (A - B)\] in RHS of the equation
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\sin ({60^ \circ } + \alpha ) = 2\left\{ {\sin \left( {({{420}^ \circ } - \alpha ) + ({{60}^ \circ } + \alpha )} \right) + \sin \left( {({{420}^ \circ } - \alpha ) - ({{60}^ \circ } + \alpha )} \right)} \right\}\]
Calculate the angle inside the brackets in RHS
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\sin ({60^ \circ } + \alpha ) = 2\left\{ {\sin \left( {{{420}^ \circ } - \alpha + {{60}^ \circ } + \alpha } \right) + \sin \left( {{{420}^ \circ } - \alpha - {{60}^ \circ } - \alpha } \right)} \right\}\]
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\sin ({60^ \circ } + \alpha ) = 2\left\{ {\sin \left( {{{480}^ \circ }} \right) + \sin \left( {{{360}^ \circ } - 2\alpha } \right)} \right\}\] … (1)
We can write \[\sin ({480^ \circ }) = \sin ({540^ \circ } - {60^ \circ })\]
From the quadrant diagram

\[\sin (3\pi - x) = \sin x\]
\[ \Rightarrow \sin ({480^ \circ }) = \sin ({60^ \circ })\]
From the table we have \[\sin {60^ \circ } = \dfrac{{\sqrt 3 }}{2}\]
\[\therefore \sin ({480^ \circ }) = \dfrac{{\sqrt 3 }}{2}\]
We can write \[\sin \left( {{{360}^ \circ } - 2\alpha } \right) = - \sin 2\alpha \] because as we move in backward direction in the quadrant diagram, value of sine becomes negative
\[\therefore \sin ({360^ \circ } - 2\alpha ) = - \sin 2\alpha \]
Substitute the values in equation (1)
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = 2\left\{ {\dfrac{{\sqrt 3 }}{2} - \sin 2\alpha } \right\}\]
\[ \Rightarrow 4\sin ({420^ \circ } - \alpha )\cos ({60^ \circ } + \alpha ) = \sqrt 3 - 2\sin 2\alpha \]
\[\therefore \] Option A is correct.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
Who is known as the "Little Master" in Indian cricket history?

Explain the Treaty of Vienna of 1815 class 10 social science CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

The highest dam in India is A Bhakra dam B Tehri dam class 10 social science CBSE

Describe the process of Unification of Italy class 10 social science CBSE

Who Won 36 Oscar Awards? Record Holder Revealed




