Question

Sides of a triangular field are $ 15m,16m $ and $ 17m $ . With the three corners of the field a cow, a buffalo and horse are tied separately with ropes of length $ 7m $ each to gaze in the field. Find the area of the field which cannot be gazed by the three animals.

Answer 1

Hint: As we know that the above given question is a word problem. A problem is a mathematical question written as one sentence or more describing a real life scenario where that problem needs to be solved by the way of mathematical calculation. We can solve the given problem by applying the method of mathematical numbers as least or highest number of multiple required.

Complete step by step solution:
We need to first understand the requirement of the question i.e. to find the area of that part of the field which cannot be gazed by the animals. First we will draw a diagram according to the question:

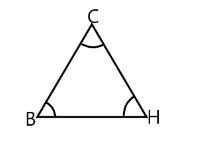
Here in the above diagram C is for Cow, B is for buffalo and H represents Horse. And let $ BH = 15m,CB = 17m $ and $ CH = 16m $ . Now we have the radius of each of the sectors $ 7m $ . Now we will find the area of sector with angle $ C $ is
$ \dfrac{{\angle C}}{{360}} \times \pi {r^2} = \dfrac{{\angle C}}{{360}} \times \pi {(7)^2} $ .
Similarly we will find the area of sector with angle $ B $ is
$ \dfrac{{\angle B}}{{360}} \times \pi {r^2} = \dfrac{{\angle B}}{{360}} \times \pi {(7)^2} $
And the area of sector with angle $ H $ is
$ \dfrac{{\angle H}}{{360}} \times \pi {r^2} = \dfrac{{\angle H}}{{360}} \times \pi {(7)^2} $ . Now we will calculate the sum of the area of these sectors
$ = \;\dfrac{{\angle C}}{{360}} \times \pi {(7)^2} + \dfrac{{\angle B}}{{360}} \times \pi {(7)^2} + \dfrac{{\angle H}}{{360}} \times \pi {(7)^2} $ ,
taking the common ones out we get
$ \dfrac{{\left( {\angle B + \angle H + \angle C} \right)}}{{360}} \times \pi \times 49 $ .
Also we know that the sum of all the angles of a triangle is always $ {180^ \circ } $ . So we can write $ (\angle B + \angle H + \angle C) = 180 $ , by substituting the value we get:
$ \dfrac{{180}}{{360}} \times \dfrac{{22}}{7} \times 49 = 77{m^2} $ .
We can now calculate the semi perimeter of the triangle,
$ s = \dfrac{{a + b + c}}{2} = \dfrac{{15 + 16 + 17}}{2} $ ,
Therefore $ s = 24 $ . We know the formula of area of triangular field i.e.
$ \sqrt {s(s - a)(s - b)(s - c)} = \sqrt {24(24 - 15)(24 - 16)(24 - 17)} $ ,
on further simplifying it gives us $ \sqrt {64 \times 9 \times 8 \times 7} = 24\sqrt {21} $ . So the area of the triangular field which cannot be gazed by all the three animals is area of triangular field – area of each sectorial field i.e. $ 24\sqrt {21} - 77{m^2} $ .
Hence the area which cannot be gazed is $ (24\sqrt {21} - 77){m^2} $ .
So, the correct answer is “ $ (24\sqrt {21} - 77){m^2} $ ”.

Note: We should always be careful what the question is asking i.e. it is asking the area of the part which cannot be gazed means the remaining part of the triangular field. Based on the requirement and by observing all the necessary information that is already available in the question we gather the information and then create an equation or by unitary method whichever is applicable, then we solve the problem and then verify the answer by putting the value in the problem and see whether we get the same answer or not.