Question

How many sides does regular polygon have, whose interior angle is eight times its exterior angle?
(a)16
(b)24
(c)18
(d)20

Answer 1

Hint: First find a formula for an interior angle in an n-sided polygon. Now you get a relation between angle and number of sides. So, by using the first condition you can derive an equation in terms of the number of sides of both the polygons. By using the second condition. Now you have 2 equations in the same variables, so by applying elimination method you can equate the both equations. Thus, getting the value of the number of sides.

Complete step-by-step answer:
As we know all angles (interior) are equal in a polygon we can write: $Interior\text{ angle}=\dfrac{Sum\text{ of interior angles}}{n}........\left( 1 \right)$. So, now we need the sum of all interior angles.

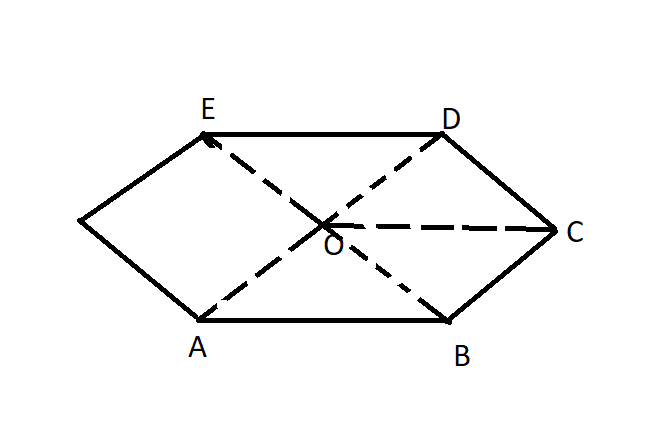
Let us take a n-sided polygon ABCDE. Take any point O inside and join OA, OB, OC,… For n-sided polygons, we get n triangles. We know sum of angles of triangles is ${{180}^{0}}$. From above statement we can say that the angles as:
Sum of all interior angles + Sum of angles of angles at O $=n\times 180$
By diagram, we can say: Sum of angles at O$={{360}^{0}}$
By substituting this and subtracting 360 on both sides, we get:
 Sum of all interior angles $=n\times 180-360$
By substituting this in equation (1), we get:
Interior angle of polygon$=\dfrac{180n-360}{n}........\left( 2 \right)$
We know the relation between exterior angle, interior angle.

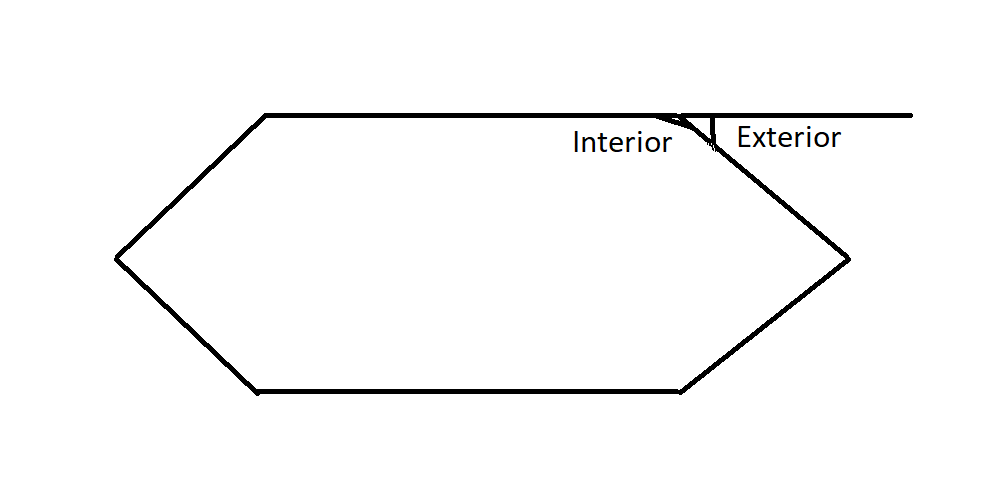
They form a straight line. So, we say:
Exterior angle $=180$
By substituting equation (2), we can write the equation:
Exterior angle$+\dfrac{180n-360}{n}=180$
By subtracting term on both sides, we can write it as:
Exterior angle$=180-\dfrac{180n-360}{n}$
By simplifying the above equation, we can write it as:
Exterior angle$=\dfrac{360}{n}$
By multiplying with 8 on both sides, we get it as:
$8\times \left( exterior\ angle \right)=8\times \dfrac{360}{n}.......\left( 3 \right)$
Given that each interior angle is 8 times the exterior.
By using elimination method, we can equate both equations (2), (3), we get it as:
$\dfrac{180n-360}{n}=8\times \dfrac{360}{n}$
By writing left hand side as 2 separate fractions we get it as:
$180-\dfrac{360}{n}=8\times \dfrac{360}{n}$
By multiplying n on both sides, we get equation in form of:
$n\times \left( 180-\dfrac{360}{n} \right)=8\times \dfrac{360}{n}\times n$
By multiplying n inside the bracket, we get it in form:
$180n-\dfrac{360}{n}\times n=8\times \dfrac{360}{n}\times n$
By simplifying the above equation, we can write it as:
$180n-360=360\times 8$
By adding 360 on both sides, we get it as:
$180n=360+360\times 8$
By taking 360 as common, we get it in the form:
$180n=360\left( 1+8 \right)$
By simplifying the above equation, we can write it as:
$180n=360\times 9$
By dividing with 180 on both sides, we get it as:
$n=\dfrac{360\times 9}{180}$
By simplifying above equation, we can write it as:
$n=2\times 9=18$
So, there are 18 sides for such a polygon given in question.
Therefore, option (c) is correct for the given question.

Note: We kept the term $360\times 8$ as it is from starting because we want to cancel the term 360 with180 on the left hand side. Even if you simplify you will get the same result. Some students confuse and think the exterior angle is 360- interior, but the wrong exterior angle of a polygon is always 180- interior. Remember this point, it's very important.