Question

What is the side of the square whose area is $25sq.cm$ ?

Answer 1

Hint: First, assume a variable $x$ in the centimeters because we don’t know the length of the sides of the square. Also, the area of the square will be ${x^2}c{m^2}$ with the given area of the square and then we will solve using the given information that side of the square whose area is $25sq.cm$

Complete step-by-step solution:
Given that, there is a square with the area $25c{m^2}$ and then we have to find the length of the sides of the square too.
Let us assume the length of the sides of the square as variable $x$ and since the square has four sides as we know.
Then we plot the diagram as

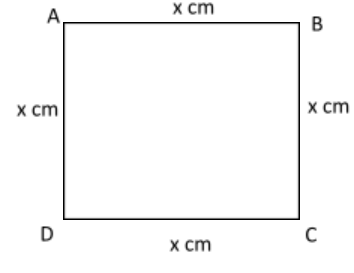
We know that the area of the square is $ = {(side)^2}$ and hence the area of the square length of whose sides are ${x^2}c{m^2}$
Since from the given, we have the area of a square given as $25c{m^2}$
Thus, equaling both the values we have ${x^2} = 25c{m^2}$
Now taking square root we get $x = 5cm$
Hence the required side of the given square is $5cm$

Note: While solving the equation ${x^2} = 25c{m^2}$ in the above solution. We have to take the positive square root only because the variable $x$ that we assume is a positive term and also it is the length of the side.
Hence the length of the side of the square cannot be negative.
Since squares have four sides and also rectangles have four sides. The only difference is in the square all the lengths of the sides are exactly equal but in the rectangle, the sides need not be equal.