Question

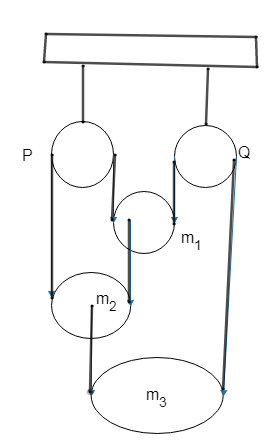
Shown in the figure in a system of three bodies of mass ${m_1},{\text{ }}{m_2}{\text{ and }}{m_3}$ connected by a single inextensible light string. If all the surfaces in contact are smooth and the pulleys P and Q are light, find the tension in the string.

Answer 1

Hint: Consider the pulley P and Q as light and thus their effect can be neglected. Then apply Newton’s laws of motion to find the acceleration and then find the tension in the string for the case of three bodies ${m_1},{\text{ }}{m_2}{\text{ and }}{m_3}$ connected by light string.

Complete answer:
Since all the strings are connected to each other, it will have some of the tension at all point, let it be T. Consider the acceleration of pulley is ${a_1},{\text{ }}{a_2}{\text{ and }}{a_3}$ downwards.

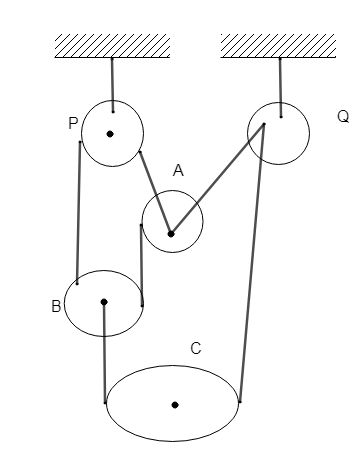
According to the constraint equation,
$\eqalign{
  & \sum T.a = 0 \cr
  & - 2T{a_3} - T.{a_2} - T{a_1} = 0 \cr
  & 2{a_3} + {a_2} + {a_1} = 0......\left( 1 \right) \cr} $
Now, applying newton, laws on each block we get,
$\eqalign{
  & 10 - 2T = {a_3}......\left( 2 \right) \cr
  & 10 - T = {a_2}.......(3) \cr
  & 10 - T = {a_1}.......\left( 4 \right) \cr} $
From equation (2) and (3), we get
$\eqalign{
  & - T = {a_3} - {a_2} \cr
  & \Rightarrow T = {a_2} - {a_3}......\left( 5 \right) \cr} $
Put it in
$\eqalign{
  & 10 - {a_2} + {a_3} = {a_2} \cr
  & \Rightarrow 2{a_2} = 10 + {a_3}.....\left( 6 \right) \cr} $
Solving (2) and (4) we get,
$\eqalign{
  & {a_1} = {a_2} = \dfrac{{10}}{3} \cr
  & \Rightarrow {a_3} = \dfrac{{ - 10}}{3} \cr} $
Substituting the calculated values of ${a_2}$ and ${a_3}$in equation (5) we get:
$\eqalign{
  & T = {a_2} - {a_3} \cr
  & \Rightarrow T = \dfrac{{10}}{3} - \left( {\dfrac{{ - 10}}{3}} \right) \cr
  & \Rightarrow T = \dfrac{{10}}{3} + \dfrac{{10}}{3} \cr
  & \therefore T = \dfrac{{20}}{3}N \cr} $
Therefore, the tension acting on the string is $\dfrac{{20}}{3}$ Newtons.

Note:
There are three statements by Newton which are considered as the three laws of motion. These statements are:
1. If the vector sum of all the forces acting on a given particle is zero then and only then the particle remains unaccelerated (i.e. remains at rest or moves with constant velocity.
2. The acceleration of a particle as measured from an inertial frame of reference is given by the vector sum of all the forces acting on the particle divided by its mass.
3. If a body exerts a force F on another body B, then the body B also exerts a force -F on the first body A. This in simpler words is known as every action has an equal and opposite reaction.