Question

Show using trigonometric identities that $\cos \left( {{35}^{\circ }}+A \right)\cos \left( {{35}^{\circ }}-B \right)+\sin \left( {{35}^{\circ }}+A \right)\sin \left( {{35}^{\circ }}-A \right)=\cos \left( A+B \right)$ where $A,B$ are angles.

Answer 1

Hint: We recall the definition of sine and cosine of an angle in a right angled triangle. We recall the cosine of angle difference formula that if there are two angles with measure $\alpha $ and $\beta $ with condition $\alpha >\beta $then cosine of their difference is given by $\cos \left( \alpha -\beta \right)=\cos \alpha \cos \beta +\sin \alpha \sin \beta $. We take $\alpha ={{35}^{\circ }}+A$ and $\beta ={{35}^{\circ }}-B$ and use the formula.

Complete step-by-step answer:

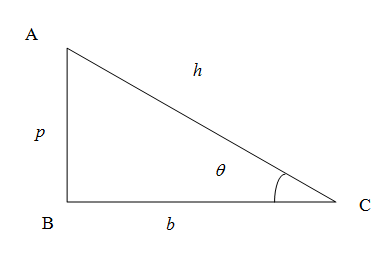
We know that in right angled triangle the side opposite to right angled triangle is called hypotenuse denoted as $h$, the vertical side is called perpendicular denoted as $p$ and the horizontal side is called the base denoted as $b$.\[\]
We know from the trigonometric ratios in a right angled triangle the sine of any angle is given by the ratio of side opposite to the angle to the hypotenuse. In the figure the sine of the angle $\theta $ is given by
\[\sin \theta =\dfrac{p}{h}\]
Similarly the cosine of an angle is the ratio of side adjacent (also called leg adjacent ) to the angle (excluding hypotenuse) to the hypotenuse. So we have cosine of angle $\theta $
\[\cos \theta =\dfrac{b}{h}\]
We know from cosine of angle difference formula that if there are two angles with measure $\alpha $ and $\beta $ with condition $\alpha >\beta $then cosine of their difference is given by
\[\cos \left( \alpha -\beta \right)=\cos \alpha \cos \beta +\sin \alpha \sin \beta \]
We are asked in the question to prove the following statement
\[\cos \left( {{35}^{\circ }}+A \right)\cos \left( {{35}^{\circ }}-B \right)+\sin \left( {{35}^{\circ }}+A \right)\sin \left( {{35}^{\circ }}-A \right)=\cos \left( A+B \right)\]
Here $A$ and $B$ measure of angles in degree unit. We observe the left hand side of the statement and see that it is expression similar to the expression of cosine of angle difference formula with angles ${{35}^{\circ }}-A$ and ${{35}^{\circ }}+A$. We use cosine of angle difference formula $\alpha ={{35}^{\circ }}+A$ and $\beta ={{35}^{\circ }}-B$ and proceed from left hand side to have,
\[\begin{align}
  & \Rightarrow \cos \left( {{35}^{\circ }}+A-\left( {{35}^{\circ }}-B \right) \right) \\
 & \Rightarrow \cos \left( {{35}^{\circ }}+A-{{35}^{\circ }}+B \right) \\
 & =\cos \left( A+B \right) \\
\end{align}\]
The above expression is at the right hand side and hence the statement is proved.

Note: We must be careful of the confusion between cosine of angle difference formula and sine of angle difference formula which is given by $\sin \left( \alpha -\beta \right)=\sin \alpha \cos \beta -\cos \alpha \sin \beta $. If the angles are added instead of subtracted, then we call the formula cosine compound angle or angle sum formula and it is given by $\cos \left( \alpha +\beta \right)=\cos \alpha \cos \beta -\sin \alpha \sin \beta $.