
How do you show that $x + 7$ is a factor of ${x^3} - 37x + 84$ . then factor completely?
Answer
542.4k+ views
Hint:In this question, we want to prove whether $x + 7$ is the factor of the given equation. For that equate $x + 7$ to zero which will give $x = - 7$. Put this value in the given equation, if we get zero then $x + 7$ is a factor of the equation. After that divide the equation with $x + 7$ . We will get the quadratic equation which we can easily solve by the factoring method.
Complete step by step solution:
We are provided with the equation ${x^3} - 37x + 84$
Firstly, proving that whether $x + 7$ is a factor of the given equation. For that putting $x = - 7$ in the
given equation.
$
{\left( { - 7} \right)^3} - 37\left( { - 7} \right) + 84 \\
= - 343 + 259 + 84 \\
= - 343 + 343 \\
= 0 \\
$
Which proves that $x + 7$ is one factor for the given equation.
Now, we have to find the other two factors. For that dividing the ${x^3} - 37x + 84$ by $x + 7$ .
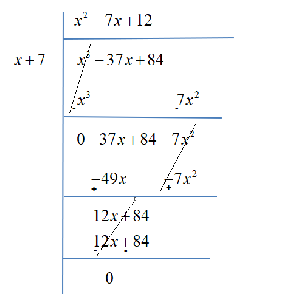
Hence, we now left with a quadratic equation ${x^2} - 7x + 12 = 0$
Finding factors by factoring method,
$
{x^2} - 3x - 4x + 12 = 0 \\
x\left( {x - 3} \right) - 4\left( {x - 3} \right) = 0 \\
\left( {x - 3} \right)\left( {x - 4} \right) = 0 \\
\left( {x - 3} \right) = 0 \\
\left( {x - 4} \right) = 0 \\
$
Hence, factors of the above given equation are $ - 7,3,4$
Note: Solve the equation carefully. Take care of the signs while dividing the given equation by $x + 7$ . We can also use the formula for solving the quadratic equation. Make sure that the factor is firstly be checked by putting that value of x into the given equation.
Complete step by step solution:
We are provided with the equation ${x^3} - 37x + 84$
Firstly, proving that whether $x + 7$ is a factor of the given equation. For that putting $x = - 7$ in the
given equation.
$
{\left( { - 7} \right)^3} - 37\left( { - 7} \right) + 84 \\
= - 343 + 259 + 84 \\
= - 343 + 343 \\
= 0 \\
$
Which proves that $x + 7$ is one factor for the given equation.
Now, we have to find the other two factors. For that dividing the ${x^3} - 37x + 84$ by $x + 7$ .
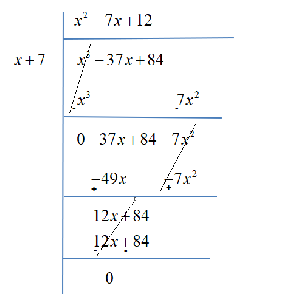
Hence, we now left with a quadratic equation ${x^2} - 7x + 12 = 0$
Finding factors by factoring method,
$
{x^2} - 3x - 4x + 12 = 0 \\
x\left( {x - 3} \right) - 4\left( {x - 3} \right) = 0 \\
\left( {x - 3} \right)\left( {x - 4} \right) = 0 \\
\left( {x - 3} \right) = 0 \\
\left( {x - 4} \right) = 0 \\
$
Hence, factors of the above given equation are $ - 7,3,4$
Note: Solve the equation carefully. Take care of the signs while dividing the given equation by $x + 7$ . We can also use the formula for solving the quadratic equation. Make sure that the factor is firstly be checked by putting that value of x into the given equation.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Explain zero factorial class 11 maths CBSE

What is a periderm How does periderm formation take class 11 biology CBSE




