Question

Show that $\vec{a}.(\vec{b} \times \vec{c})$ is equal in magnitude to the volume of the parallelepiped formed on the three vectors $\vec{a}$, $\vec{b}$, and $\vec{c}$.

Answer 1

Hint: First find the volume of the parallelepiped as the product of its length, breadth and height. Then consider three vectors to be projected along the sides of the parallelepiped and evaluate the expression given in the question by keeping in mind that the dot product pertains to the cosine of the angle between the two vectors whereas the cross product comes from the sine of the angle between the two vectors resulting in a third vector pointing in a direction normal to both the vectors. To this end, verify the statement presented in the question.

Formula Used:
Dot product: $\vec{a}.\vec{b} = |\vec{a}||\vec{b}|cos\theta$
Cross product: $\vec{a}\times \vec{b} = |\vec{a}||\vec{b}|sin\theta\; \hat{n}$

Complete Step-by-Step Solution:
Let us consider a parallelepiped as shown in the figure.

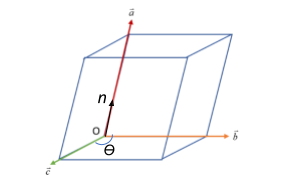
A parallelepiped is a three- dimensional figure that is formed by six faces of parallelograms.

Let us consider vectors $\vec{a}$, $\vec{b}$ and $\vec{c}$ that form the height, length and breadth sides of a parallelepiped. The magnitude of each side would be $|\vec{a}|$, $|\vec{b}|$ and $|\vec{c}|$ respectively. Therefore, the volume of the parallelepiped would be the product of its length, breadth and height, i.e.,
$V_{parallelopiped} = |\vec{a}||\vec{b}||\vec{c}|$.

Now, let us evaluate the vectors expression given to us.
$\vec{a}.(\vec{b} \times \vec{c})$
$\Rightarrow \vec{a}.(|\vec{b}||\vec{c}|sin\theta\;\hat{n})$, where $\theta$ is the angle between vectors $\vec{b}$ and $\vec{c}$ as shown in the figure. The direction of the cross product between the two is indicated by a unit vector $\hat{n}$, whose $|\hat{n}|=1$

From the figure we see that $\theta$ forms a vertex angle of $90^{\circ}$ since the base is a parallelogram.
$\Rightarrow \vec{a}.(|\vec{b}||\vec{c}|sin90^{\circ}\hat{n}) = \vec{a}.(|\vec{b}||\vec{c}|(1)\hat{n}) = \vec{a}.(|\vec{b}||\vec{c}|\hat{n})$

Now, we perform a dot product between vectors $\vec{a}$ and $\hat{n}$. The two appear parallel and pointing in the same direction since the cross product of vectors $\vec{b}$ and $\vec{c}$ yielded a resultant vector directed normal to the plane containing the vectors $\vec{b}$ and $\vec{c}$.
If $\phi$ is the angle between $\vec{a}$ and $\hat{n}$, then $\phi=0^{\circ}$
$\Rightarrow \vec{a}.(|\vec{b}||\vec{c}|\hat{n}) = \vec{a}.\hat{n} cos\phi |\vec{b}||\vec{c}|$
$= |\vec{a}||\hat{n}|cos0^{\circ}|\vec{b}||\vec{c}| = |\vec{a}|(1)(1) |\vec{b}||\vec{c}|$
$= |\vec{a}||\vec{b}||\vec{c}| = V_{parallelopiped}$

We have thus proved that $\vec{a}.(\vec{b} \times \vec{c})$ is equal in magnitude to the volume of the parallelepiped formed on the three vectors $\vec{a}$, $\vec{b}$, and $\vec{c}$.

Note:
Do not get confused between the dot product and the cross product of vectors.
The dot product is the product of the magnitudes of the vectors and the cosine of the angle between them whereas the cross product is the product of the magnitude of the vectors and the since of the angle between them. Consequently, the dot product of orthogonal vectors is zero whereas the cross product of orthogonal vectors is the maximum. The resultant vector of a dot product is a projection of the two vectors whereas the cross product represents a third vector normal to the plane containing the two vectors. The result of a dot product is a scalar quantity whereas the cross product produces a vector quantity.