Question

Show that the value of \[\sin \theta \text{ and }\cos \theta \] cannot be more than 1.

Answer 1

Hint:First of all, consider a triangle ABC, right-angled at B and \[\angle C=\theta \], AB = a and BC = b. Now, find AC by using the Pythagoras theorem. Now, use \[\sin \theta =\dfrac{perpendicular}{hypotenuse}=\dfrac{AB}{AC}\] and \[\cos \theta =\dfrac{base}{hypotenuse}=\dfrac{BC}{AC}\] and examine these values to prove the desired result.

Complete step-by-step answer:
In this question, we have to show that the value of \[\sin \theta \text{ and }\cos \theta \] cannot be more than 1. Let us first understand the trigonometric ratios \[\sin \theta \] and \[\cos \theta \] from basic. When we look from the vertex with angle \[\theta \], \[\sin \left( \theta \right)\] is the ratio of the opposite side (perpendicular) to the hypotenuse. Similarly, when we look from the vertex with angle \[\theta ,\cos \theta \] is the ratio of the adjacent side (base) to the hypotenuse.
Let us consider a triangle ABC, right-angled at B.
Figure 1:

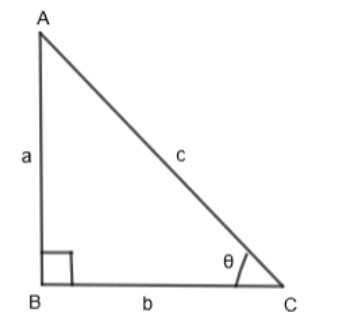
In the above right-angled triangle ABC,
\[\angle B={{90}^{o}}\]
\[\angle C=\theta \]
AB = a
BC = b
We know that Pythagoras theorem states that in a right-angled triangle, the square of the hypotenuse side is equal to the sum of the squares of the other two sides. So, in the above triangle ABC, by applying Pythagoras theorem, we get,
\[{{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}={{\left( AC \right)}^{2}}\]
Now by substituting the value of AB = a and BC = b, we get,
\[{{a}^{2}}+{{b}^{2}}=A{{C}^{2}}\]
\[AC=\sqrt{{{a}^{2}}+{{b}^{2}}}\]
Now, with respect to angle \[\theta \], we know that,
\[\sin \theta =\dfrac{Perpendicular}{Hypotenuse}=\dfrac{AB}{AC}.....\left( i \right)\]
\[\cos A=\dfrac{Base}{Hypotenuse}=\dfrac{BC}{AC}....\left( ii \right)\]
Now, by substituting the values of AB = a, BC = b, and AC \[=\sqrt{{{a}^{2}}+{{b}^{2}}}\] in equation (i) and (ii), we get,
\[\sin \theta =\dfrac{AB}{AC}=\dfrac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}}}....\left( iii \right)\]
\[\cos \theta =\dfrac{BC}{AC}=\dfrac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}}}....\left( iv \right)\]
We know that in a right-angled triangle, the hypotenuse is the longest side out of all the three sides. So, in equation (iii), we get,
\[\sqrt{{{a}^{2}}+{{b}^{2}}}>a\]
Also, in equation (iv), we get,
\[\sqrt{{{a}^{2}}+{{b}^{2}}}>b\]
We know that when the denominator is greater than the numerator in a given fraction, that fraction is always less than 1.
So, we get,
\[\sin \theta =\dfrac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}}}<1....\left( v \right)\]
\[\cos \theta =\dfrac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}}}<1....\left( vi \right)\]
For example, let us take a triangle with a = 3, b = 4 as follows:
Figure 2:

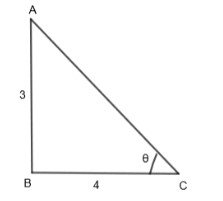
From the Pythagoras theorem, we get,
\[AC=\sqrt{{{a}^{2}}+{{b}^{2}}}\]
\[AC=\sqrt{{{\left( 3 \right)}^{2}}+{{\left( 4 \right)}^{2}}}=\sqrt{25}\]
\[AC=5\]
So, we get,
\[\sin \theta =\dfrac{AB}{AC}=\dfrac{3}{5}\]
\[\cos \theta =\dfrac{BC}{AC}=\dfrac{4}{5}\]
which are lesser than 1.
Also, in figure 1, in an ideal case, when we take \[\theta ={{90}^{o}}\], we can see that AB = AC as both would be parallel. So,
\[\sin \theta =\dfrac{AB}{AC}=1...\left( vii \right)\]
So, from equation (v) and (vii), we get,
\[\sin \theta \le 1\]
Also, in figure 1, in an ideal case, when we take \[\theta ={{0}^{o}}\], AC and BC will get overlapped, so we can see that AC = BC. So,
\[\cos \theta =\dfrac{BC}{AC}=1...\left( viii \right)\]
So, from equation (vi) and (viii), we get,
\[\cos \theta \le 1\]
So, we have proved that the values of \[\sin \theta \text{ and }\cos \theta \] are always less than or equal to 1 or in other words we have proved that \[\sin \theta \text{ and }\cos \theta \] cannot be more than 1.

Note: In this question, many students take only the practical case when hypotenuse is the longest side and leave out the ideal case when the hypotenuse is equal to one of the sides. So, this must be taken care of because \[\sin {{90}^{o}}=1\] and \[\cos {{0}^{o}}=1\] is as useful as the other angles while dealing with the questions related to geometry.