Question

Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is ${\cos ^{ - 1}}\dfrac{1}{{\sqrt 3 }}.$

Answer 1

Hint: In order to prove this question we will find the maxima of value by differentiating the volume. By this we will get the value of h and with the help of figure we will create a relation between semi-vertical angle, height and slant height. By using these properties we will get the answer.

Complete step-by-step answer:

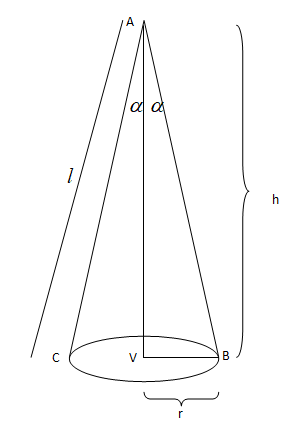
Let us consider the following variables
h= height of cone
l= slant height of cone
r= radius of cone
$\alpha $ =semi vertical angle of the cone
Let us assume that “V” is the volume of the cone which has to be maximized.
We know that
\[V = \dfrac{1}{3}\pi {r^2}h.........(1)\]
From the figure, we have
$
   \Rightarrow {l^2} = {r^2} + {h^2} \\
   \Rightarrow {l^2} - {h^2} = {r^2} \\
$
On substituting the value of ${r^2}$ in equation (1), we get
\[V = \dfrac{1}{3}\pi ({l^2} - {h^2})h = \dfrac{1}{3}\pi ({l^2}h - {h^3})\]
On differentiating with respect to h, we get
$\dfrac{{dV}}{{dh}} = \dfrac{1}{3}\pi ({l^2} - 3{h^2})..............(2)$
For maximum volume of V, let us put \[\dfrac{{dV}}{{dh}} = 0\]
So, from equation (2), we have
$
   \Rightarrow \dfrac{1}{3}\pi ({l^2} - 3{h^2}) = 0 \\
   \Rightarrow {l^2} - 3{h^2} = 0 \\
   \Rightarrow {h^2} = \dfrac{{{l^2}}}{3} \\
   \Rightarrow h = \dfrac{l}{{\sqrt 3 }}{\text{ }}\left[ {\because h,l > 0} \right] \\
$
Again, differentiating equation (2) with respect to h, we get
$
   \Rightarrow \dfrac{{{d^2}V}}{{d{h^2}}} = \dfrac{1}{3}\pi ( - 6h) = - 2\pi h \\
   \Rightarrow {\left( {\dfrac{{{d^2}V}}{{d{h^2}}}} \right)_{h = \dfrac{l}{{\sqrt 3 }}}} = - 2\pi \dfrac{l}{{\sqrt 3 }} < 0 \\
$
Thus, the volume of the cone is maximum at $h = \dfrac{l}{{\sqrt 3 }}$
From the figure, we have
$
   \Rightarrow \cos \alpha = \dfrac{h}{l} \\
   \Rightarrow \cos \alpha = \dfrac{l}{{l\sqrt 3 }} = \dfrac{1}{{\sqrt 3 }} \\
   \Rightarrow \alpha = {\cos ^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right) \\
$
Therefore, the semi vertical angle is ${\cos ^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right)$

Note: In order to solve these types of questions, you must have a good concept of trigonometry, differentiation and functions. In order to calculate the maxima or minima of a function we use double differentiation rule which tells that after double differentiating and putting the value, if double differentiation is negative then the function has maximum value at that point and if it is positive then then the function has minima at that point. Sometimes double differentiation, so we have to use a wavy curve method to find maxima or minima.