Question

Show that the semi-vertical angle of a cone of maximum volume and given slant height is-
$\cos^{-1}\left(\dfrac1{\sqrt3}\right)$

Answer 1

Hint: In this question, we will use the formula for the volume of the cone to form the function, and then differentiate it in order to find the maxima and find the semi-vertical angle. The volume of cone is given by-
$\dfrac{1}{3} \pi{r}^{2} \times h$

Complete step-by-step solution -

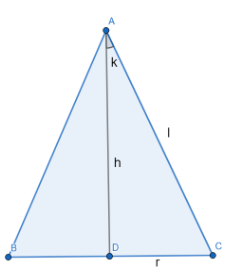
Let this be the front view of the cone, with semi-vertical angle k and given slant height l. By applying trigonometric properties, we can write that-
$h = l \cos k$
$r = l \sin k$
The volume of the cone is given by-
$\mathrm V=\dfrac13\mathrm{πr}^2\mathrm h\\\mathrm V=\dfrac13\mathrm{πsin}^2\mathrm{k cosk}$
To find the maximum value of V, we will differentiate the function V and equate it to zero. Then we can get the corresponding value of k. So-
$\dfrac{\operatorname d\mathrm V}{\operatorname d\mathrm k}=\dfrac13\mathrm\pi\left(\left(2\mathrm{sink cosk}\right)\mathrm{cosk}+\sin^2\mathrm k\left(-\mathrm{sink}\right)\right)=0\\
\Rightarrow \dfrac{\operatorname d\mathrm V}{\operatorname d\mathrm k}=\dfrac13\mathrm\pi\left(2\mathrm{sink cos}^2\mathrm k-\sin^3\mathrm k\right)=0\\
\Rightarrow \dfrac{\operatorname d\mathrm V}{\operatorname d\mathrm k}=\mathrm{sink}\left(2\cos^2\mathrm k-\sin^2\mathrm k\right)=0\\$
$\Rightarrow \sin k = 0$ or $2 \cos 2k = \sin 2k$
As angle k = 0 or k < 0 is not possible, so using $\sin^{2}k + \cos^{2}k = 1$,.
$\Rightarrow 2 \cos^{2}k = 1 -\cos^{2}k$
$\Rightarrow\cos^{2}k$ = $\dfrac{1}{3}$
$\Rightarrow\mathrm{cosk}=\dfrac{1}{\sqrt3}\\
\Rightarrow \mathrm k=\cos^{-1}\left(\dfrac{1}{\sqrt3}\right)$

This is the required answer.

Note: In this we can also satisfy the condition for maxima by proving the second differential to be less than zero. But it is not required because the minima condition is when k = 0, so the other condition will clearly become the maxima condition.