Question

Show that the quadrilateral, formed by joining the mid – points of the sides of a square is also a square.

Answer 1

Hint: We start solving the problem by recalling the definition and properties of the square. We use the fact that the midpoint of the line segment makes the line divide into two equal halves or two equal line segments. Now, we find the angles in a triangle formed by joining those midpoints and sides of the inner quadrilateral. We then use the fact that the angle of a straight line is 180° to get the value of all the angles of the inner quadrilateral. Using the values of angles and lengths of the quadrilateral, we decide what is the inner quadrilateral.

Complete step-by-step answer:
Before solving this question, we must know about squares and its properties.
SQUARE: A square is a two – dimensional shape. It is a quadrilateral, which means that it is made up of four straight lines. Here are some properties of a square.
1. All of its sides are of equal length, in other words, the length of its four sides is always equal or the same.
2. All of its angles are of 90°.
3. Its diagonals bisect each other.
4. Also, its diagonals make an angle of 90° with each other.

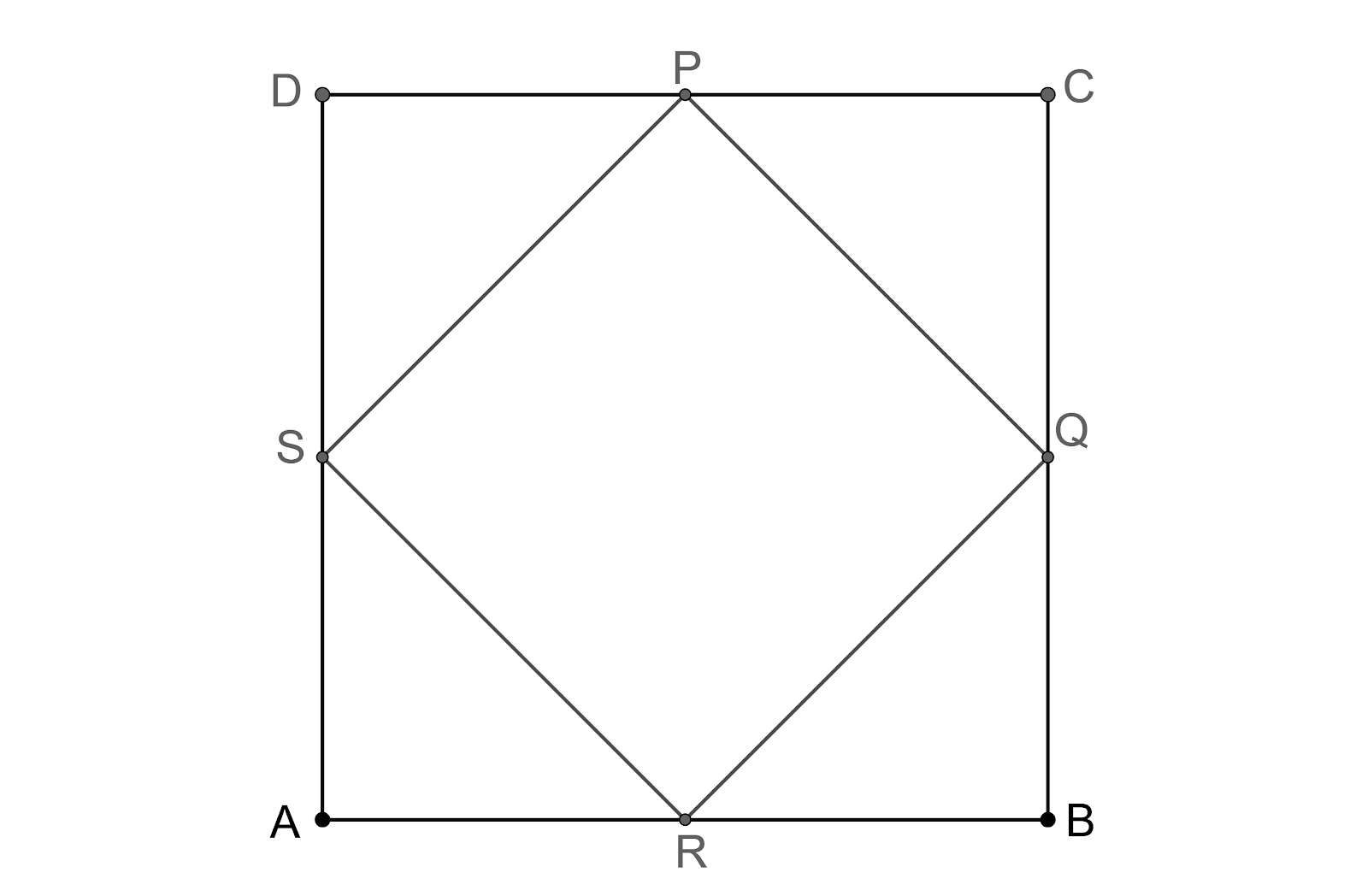
Since the points P, Q, R, S are dividing the lines CD, BC, AB, DA equally, therefore, their lengths will be equal.
As ABCD is a square, all of its angles will be right angle.

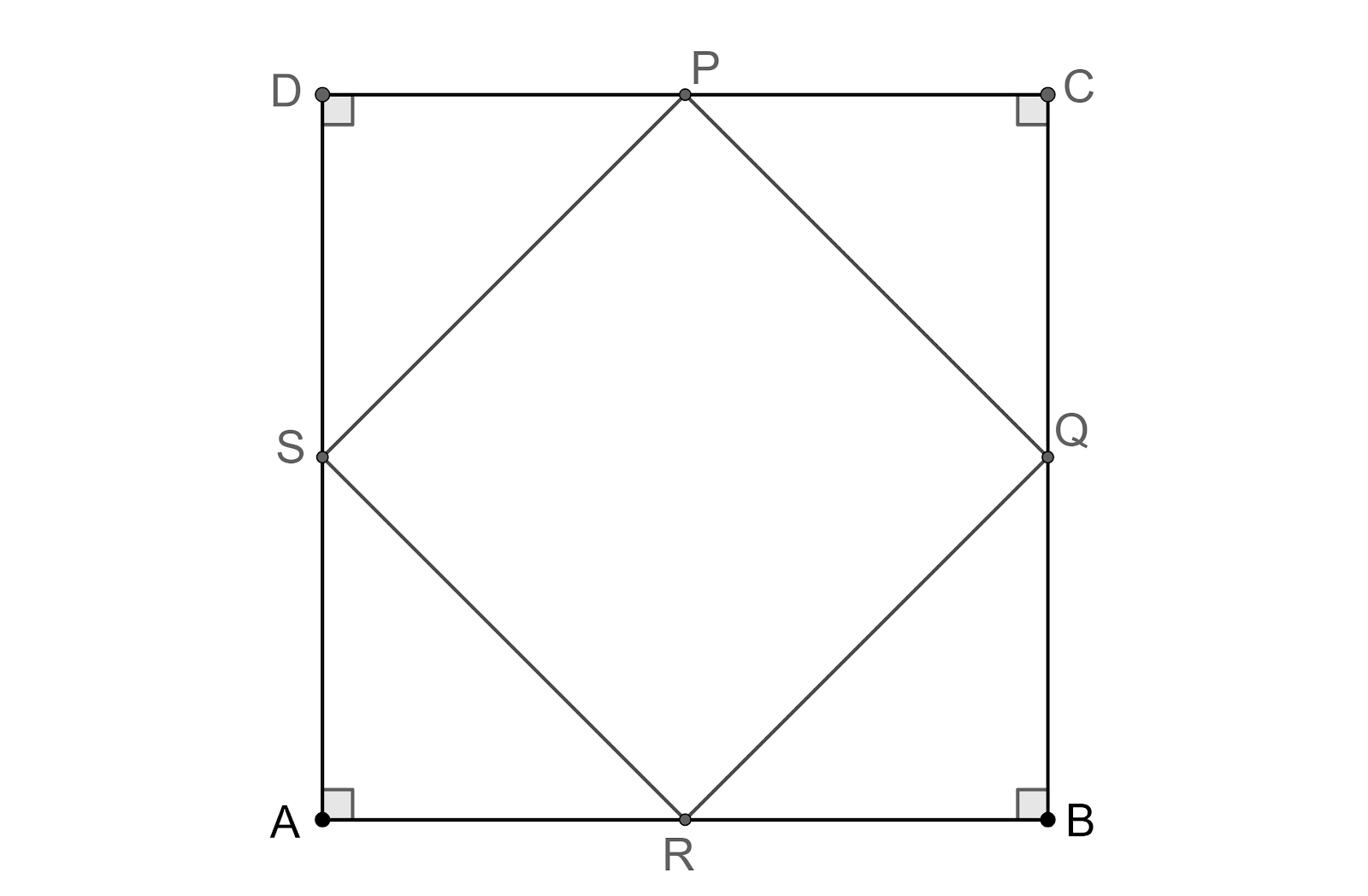
And, as we know that the straight line makes an angle of 180°.
Therefore, the angle at ‘R’ will also be 180°.

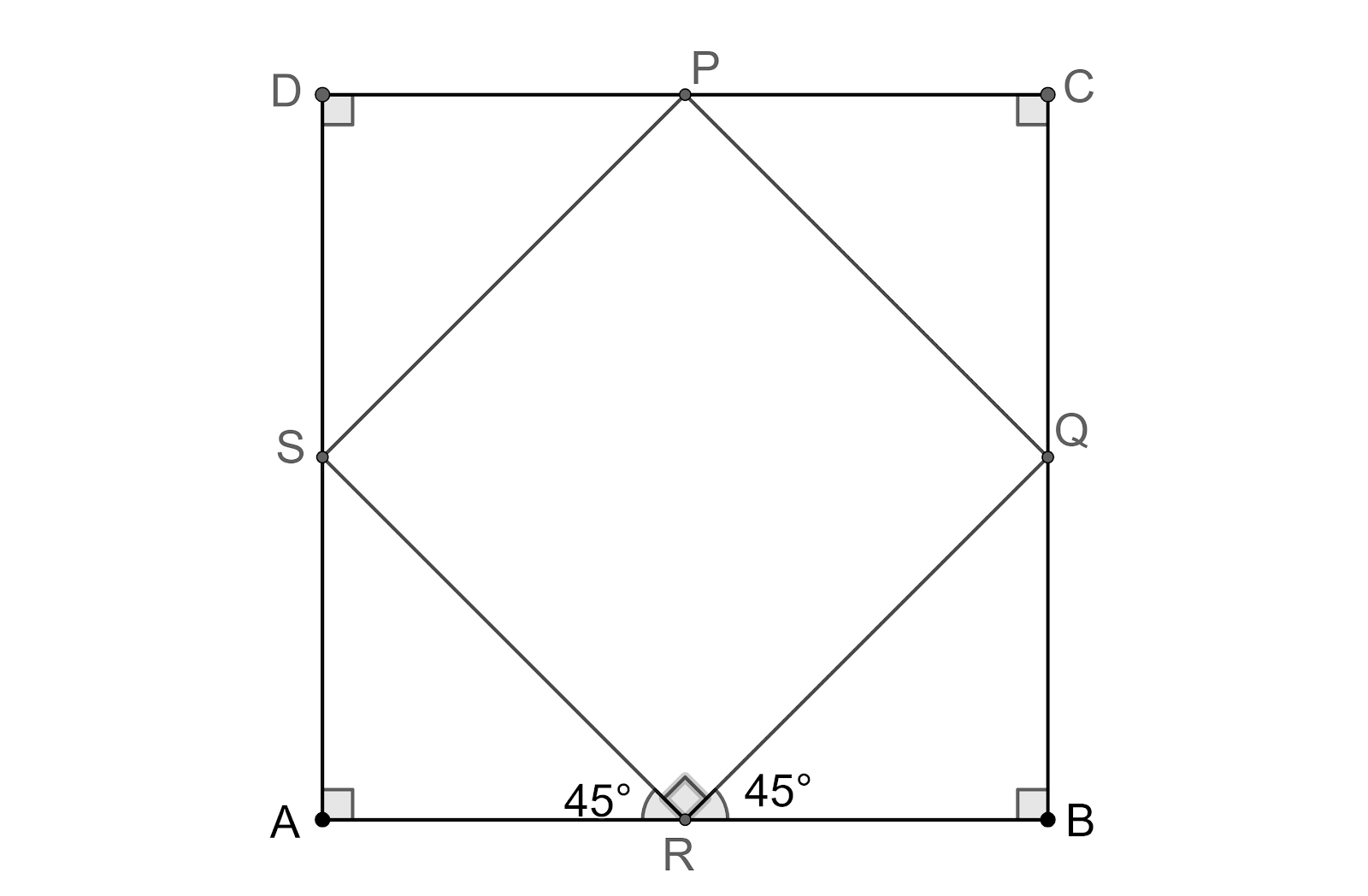
Now, as we can see, the isosceles triangle has been formed. Here we use the fact that angles opposite to equal sides are also equal and the sum of the angles in a triangle is 180°.
From triangle ARS, we have $\angle ARS=\angle SRA$ and $\angle ARS+\angle SRA+\angle RAS={{180}^{o}}$.
$\Rightarrow \angle ARS+\angle ARS+{{90}^{o}}={{180}^{o}}$.
$\Rightarrow 2\angle ARS={{180}^{o}}-{{90}^{o}}$.
$\Rightarrow 2\angle ARS={{90}^{o}}$.
$\Rightarrow \angle ARS=\dfrac{{{90}^{o}}}{2}$.
$\Rightarrow \angle ARS={{45}^{o}}$.
$\angle ARS=\angle SRA={{45}^{o}}$.
Similarly, $\angle QRB={{45}^{o}}$.
We have $\angle SRA+\angle SRQ+\angle QRB={{180}^{o}}$.
$\Rightarrow {{45}^{o}}+\angle SRQ+{{45}^{o}}={{180}^{o}}$.
$\Rightarrow \angle SRQ+{{90}^{o}}={{180}^{o}}$.
$\Rightarrow \angle SRQ={{180}^{o}}-{{90}^{o}}$.
$\Rightarrow \angle SRQ={{90}^{o}}$.
Now, applying Pythagoras Theorem, we will be able to find the value of QR, SR, SP, and PQ.
Let us assume the length of QC to be ‘x’. Therefore, the length of RC will also be ‘x’. And let us assume that QR is ‘y’. So, applying the Pythagoras theorem, we will get:
\[\Rightarrow {{(x)}^{2}}+{{\left( x \right)}^{2}}={{\left( y \right)}^{2}}\].
\[\Rightarrow 2{{\left( x \right)}^{2}}={{\left( y \right)}^{2}}\].
\[\Rightarrow \sqrt{2}x=y\].
Now, if we will repeat the same process will SR, SP and PQ, then we will find that their length will also be
$\sqrt{2}x$.
And, as the lengths of QR, SR, SP and PQ will be equal to $\sqrt{2}x$, therefore, all of them will equal to each other.
Hence, we can now say that PQRS is a square, because:-
QR = SR = SP = PQ = $\sqrt{2}x$.
Angle P = Angle Q = Angle R = Angle S = \[{{90}^{\circ }}\]
And only a square has all of these properties.

Note: We should not just find the length of all the sides of the quadrilateral are equal and conclude it as square. Because, it is not the only criteria for becoming a square as rhombus has length of all sides equal. We should always check properties of both sides and angles of the given quadrilateral in order to conclude it as a square or rectangle or others. We should keep in mind that the angles opposite to the equal sides in a triangle are also equal.