Question

Show that the points representing the complex numbers $7 + 9i, - 3 + 7i,3 + 3i$ form a right-angled triangle on the argand diagram.

Answer 1

Hint: The Argand plane is the plane representing the complex numbers, the complex plane or the argand plane is just like the Cartesian plane, but instead of the two-axis which represents an ordered pair in an argand plane the horizontal axis represents the real part of the complex numbers and the vertical axis is the representative of the imaginary part of the complex number. We will have to show that these points when plotted on an argand plane are forming a right-angled triangle. We can show that with the help of using the distance between two points and applying the Pythagoras theorem to check if the points are right-angled triangles or not.

Complete step-by-step answer:
We will first plot these given points on the argand plane,
 

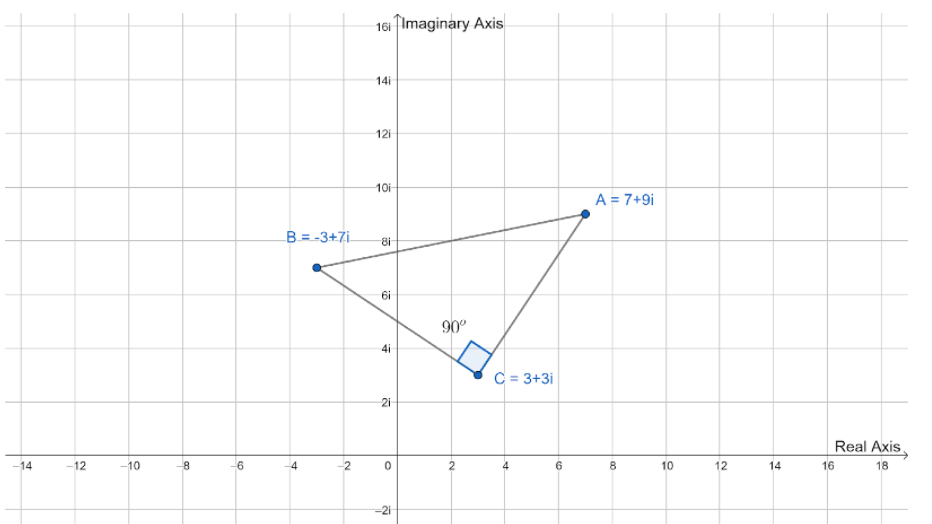
Now, find the distance between these points much akin to the distance between two points on the Cartesian plane
The respective distances between the three vertices will now be found and then we will proceed to apply the Pythagoras theorem so as to prove that these points are indeed lying on the vertices of a right-angled triangle.
The distance between point $A = 7 + 9i$ and $B = - 3 + 7i$, $C = 3 + 3i$, are calculated as,
$ \Rightarrow AB = |7 + 9i - ( - 3 + 7i)|$
$ \Rightarrow AB = |10 + 2i|$
$ \Rightarrow AB = \sqrt {{{10}^2} + {2^2}} $
$ \Rightarrow AB = \sqrt {104} $
Now finding $BC$,
$ \Rightarrow BC = | - 3 + 7i - (3 + 3i)|$
$ \Rightarrow BC = | - 6 + 4i|$
$ \Rightarrow BC = \sqrt {{{( - 6)}^2} + {4^2}} $
$ \Rightarrow BC = \sqrt {52} $
At last, finding $CA$.
$ \Rightarrow CA = |3 + 3i - (7 + 9i)|$
$ \Rightarrow CA = | - 4 - 6i|$
$ \Rightarrow CA = \sqrt {{{( - 4)}^2} + {{( - 6)}^2}} $
$ \Rightarrow CA = \sqrt {52} $
Since we can see that $A{B^2} = C{A^2} + B{C^2}$ that is :
$ \Rightarrow {(\sqrt {104} )^2} = {(\sqrt {52} )^2} + {(\sqrt {52} )^2}$
$ \Rightarrow 104 = 52 + 52$
$ \Rightarrow 104 = 104$
Equation Satisfied.
We can write that they follow Pythagoras theorem and thus all the points form the shape of a right-angled triangle.

Note: The modulus of the complex number gives the absolute value of that complex number known as its modulus, this modulus function is the function that can give us the distance of a point from the origin. Hence the more the modulus of a complex number the farther it is from the centre of the argand plane.
The modulus of a complex number of the form,$Z = a + ib$, is $|Z| = \sqrt {{a^2} + {b^2}} $,
Where $a$ and $b$ are the real and imaginary parts of the complex numbers.