Question

Show that the points $A\left( -5,1 \right),B\left( 5,5 \right)\ and\ C\left( 10,7 \right)$are collinear.

Answer 1

Hint: We will be using the concept of coordinate geometry to solve the problem. We will be using the fact that if three points are collinear then the slope of any two pairs of points is the same.

Complete step-by-step answer:
Now, we have been given three points as,
$A\left( -5,1 \right),B\left( 5,5 \right)\ and\ C\left( 10,7 \right)$

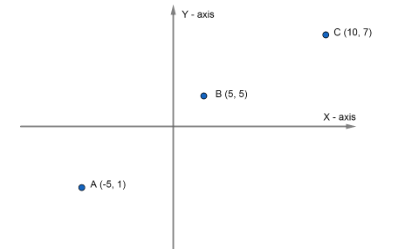
Now, we know that the slope of line having $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$as a coordinate is $slope=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$.
Now, we have the slope of AB is,
$\begin{align}
  & slope\ of\ AB\ =\dfrac{5-1}{-5-5} \\
 & =\dfrac{4}{10} \\
 & =\dfrac{2}{5} \\
\end{align}$
Also, the slope of BC is,
$\begin{align}
  & slope\ of\ BC\ =\dfrac{7-5}{10-5} \\
 & =\dfrac{2}{5} \\
\end{align}$
Now, we can see that the slope of AB and BC is the same. So, we can say that A, B and C lie in a line. Also, we know that if three points lie on a line then they are collinear.

Note: Another approach to this question is we can use distance formulas to find the distance between the points AB ,AC and BC and equate AB+BC to AC to show the collinearity.