Question

Show that the moment of a couple does not depend upon the point about which you take the moment.

Answer 1

Hint:As we define the moment of couple it Is the product of the force and the distance perpendicular between the line of action. As we are going to show that it does not depend on the point about which we take the moment. We will use formula $ F \times d$ to proceed, here $F$ is the force acting and $d$ it is the perpendicular distance.

Complete step by step answer:
In this case to prove the point that the moment of a couple is constant and does not depend upon the point about which we take the moment. We need to demonstrate the couple in a diagram for better understanding.

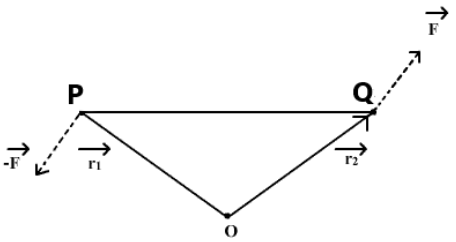
From the diagram we can interpret, a couple is considered acting on a rigid body at points P and $Q$. The position vectors at these points are $ \overrightarrow {{r_1}} \,and\,\overrightarrow {{r_2}} $ with respect to the origin $O$. As it is the moment of a couple the forces acting at point $P$ and $Q$ will be given as $ - \overrightarrow F ,\overrightarrow F$. We can then find out the moment of this couple using the forces and the position vectors as follows.

The moment of couple = Moment of force at P + Moment of force at Q
\[\text{The moment of couple =}\overrightarrow {{r_1}} \times (\overrightarrow { - F} ) + \overrightarrow {{r_2}} \times (\overrightarrow F ) \\
\Rightarrow \left( {\overrightarrow {{r_2}} - \overrightarrow {{r_1}} } \right) \times \overrightarrow F \\ \]
Triangle law but from the diagram we have,
$\overrightarrow {{r_1}} + \overrightarrow {PQ} = \overrightarrow {{r_2}} ....(triangle\,law) \\
\overrightarrow {{r_2}} - \overrightarrow {{r_1}} = \overrightarrow {PQ} \\ $
$\text{Moment of a couple} = \overrightarrow {PQ} \times \overrightarrow F $
As we see and get from the above equation, the moment of the couple which we found out is independent of origin. Here, origin is the point about which we take the moment of forces.Hence proved.

Note:If we go further, the moment of a couple is independent of the point on the plane and same for all points in the plane. This is the mechanics used in the operation of steering and other applications such as key in lock, see-saw, etc. in which we need to provide a couple for output.