Question

Show that the locus of a point, which is such that the tangents from it to two given concentric circles are inversely as the radii, is a concentric circle, the square of whose radius is equal to the sum of the squares of the radii of the given circles.

Answer 1

Hint:- Assume the concentric circles to be centred at origin. And assume that the locus of the point which we had to find is (h, k) and also find the distance of point (h,k) from the two given circles.

Complete step-by-step solution -

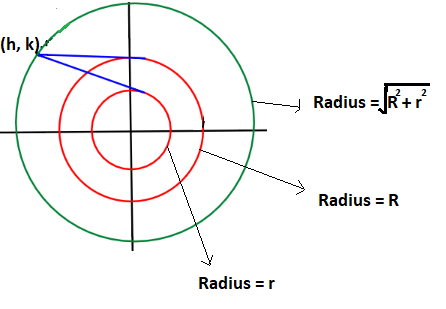
Now, for our convenience, we take the concentric circles to be centred at
origin with radius R, r such that ${\text{R}} > {\text{r}}$.
So, let C1 and C2 be the equation of two circles. Then,
$
   \Rightarrow {\text{C}}1:\;{\text{ }}\;{x^2} + {y^2} = {R^2} \\
   \Rightarrow {\text{C}}2:\;{\text{ }}\;{x^2} + {y^2} = {r^2} \\
 $
Let, the point that satisfies the given condition be ${\text{(h,k)}}{\text{.}}$
As, we know that length of tangent from point ${\text{(a,b)}}$ to the circle ${x^2} + {y^2} = {c^2}$ is:
$ \Rightarrow l = \sqrt {{a^2} + {b^2} - {c^2}} $
So, length of tangent from point ${\text{(h,k)}}$to the circle C1 will be,
$ \Rightarrow {l_R} = \sqrt {{h^2} + {k^2} - {R^2}} $
And, length of tangent from point ${\text{(h,k)}}$to the circle C2 will be,
$ \Rightarrow {l_r} = \sqrt {{h^2} + {k^2} - {r^2}} $
And according to the question:
$ \Rightarrow \dfrac{R}{r} = \dfrac{{\sqrt {{h^2} + {k^2} - {r^2}} }}{{\sqrt {{h^2} + {k^2} - {R^2}} }}$ ……………………………….. (1)
Now, for solving equation 1.
We square both sides of the equation 1 and then cross-multiply. It becomes,
$ \Rightarrow {{\text{R}}^2}\left( {{h^2} + {k^2} - {R^2}} \right) = {r^2}\left( {{h^2} + {k^2} - {r^2}} \right)$
Now, solving the above equation. We get,
$ \Rightarrow \left( {{R^2} - {r^2}} \right)\left( {{h^2} + {k^2}} \right) = {R^4} - {r^4}$ ………………………. (2)
As we know that, ${R^{2n}} - {r^{2n}} = \left( {{R^n} + {r^n}} \right)\left( {{R^n} - {r^n}} \right)$
So, equation 2 becomes.
$ \Rightarrow {h^2} + {k^2} = {R^2} + {r^2}$
Now, replacing h with x and k with y. Above equation becomes,
$ \Rightarrow {x^2} + {y^2} = {R^2} + {r^2}$
So, the radius of the green circle in the above figure will be \[\sqrt {{R^2} + {r^2}} \].
$ \Rightarrow $Hence, from the above equation we see that the locus of a point, which is such that the
tangents from it to two given concentric circles are inversely, as their radii, is a concentric circle,
and the square of whose radius is equal to the sum of the squares of the radii of the given circles.
Hence proved.

Note:- Whenever we come up with this type of problem then first, we find the length of tangents, and then compare that according to the given condition then after solving the equation we will get the required equation of the circle. From that we can find the radius of the circle.