Question

Show that the length of any focal chord of a conic is a third proportional to the transverse axis and the diameter parallel to the chord.

Answer 1

Hint: First of all, consider the general equation of the conic and consider a chord on the conic and find out its length. Convert the obtained fractions into ratio and proportions to prove the problem.

Complete step-by-step answer:
Let the conic be
\[\dfrac{l}{r} = 1 - e\cos \theta \]

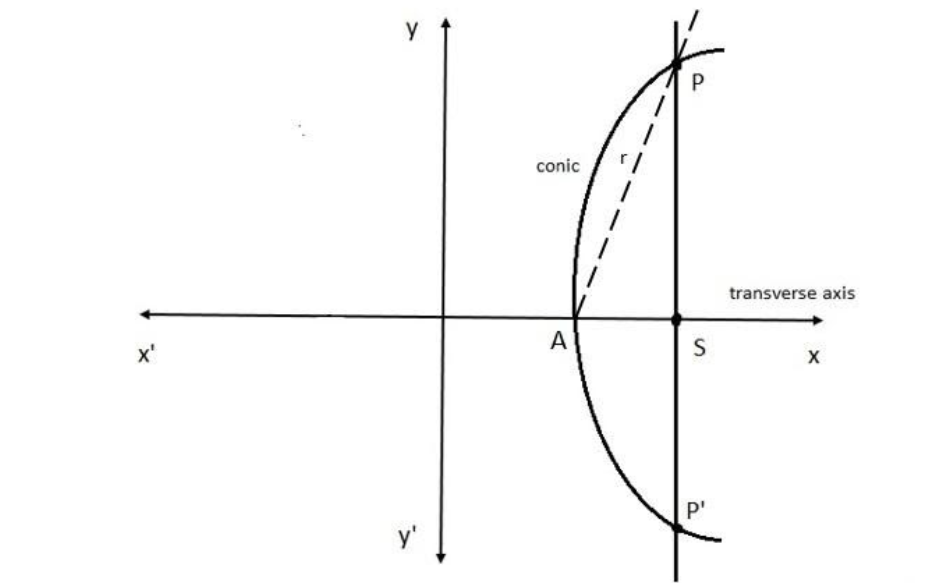
Where \[\angle PAS = \theta \]
Here \[r\] is the radius vector of any point and the diameter through the point (say \[P\]) will be \[2r\].
As we know that \[{r^2} = \dfrac{{{a^2}{b^2}}}{{{b^2}{{\cos }^2}\theta + {a^2}{{\sin }^2}\varphi }}\] where \[a\] is the length of the major axis and \[b\] is the length of the minor axis.
Hence
\[ \Rightarrow {x^2} = {\left( {2r} \right)^2} = 4{r^2} = \dfrac{{4{a^2}{b^2}}}{{{b^2}{{\cos }^2}\theta + {a^2}{{\sin }^2}\theta }}.........................................\left( 1 \right)\]
Let \[PSP'\] be any chord on the conic then we have
\[PS = \dfrac{l}{{1 - e\cos \theta }}\] and \[P'S = \dfrac{l}{{1 - e\cos \left( {\pi + \theta } \right)}} = \dfrac{l}{{1 + e\cos \theta }}\]
Let the length of the chord \[PSP'\] be \[y\], then we have
\[
   \Rightarrow y = PS + P'S \\
   \Rightarrow y = \dfrac{l}{{1 - e\cos \theta }} + \dfrac{l}{{1 + e\cos \theta }} = \dfrac{{2l}}{{1 - {e^2}{{\cos }^2}\theta }}..............................\left( 2 \right) \\
\]
Again, in a conic we have
\[{b^2} = {a^2}\left( {1 - {e^2}} \right)\]
Which can be written as
\[ \Rightarrow {e^2} = 1 - \dfrac{{{b^2}}}{{{a^2}}} = \dfrac{{{a^2} - {b^2}}}{{{a^2}}}{\text{ and }}2l = \dfrac{{2{b^2}}}{a}.............................\left( 3 \right)\]
Substituting (3) in (2), we get
\[
   \Rightarrow y = \dfrac{{\dfrac{{2{b^2}}}{a}{a^2}}}{{{a^2} - \left( {{a^2} - {b^2}} \right){{\cos }^2}\theta }} \\
   \Rightarrow y = \dfrac{{2{b^2}a}}{{{a^2}\left( {1 - {{\cos }^2}\theta } \right) + {b^2}{{\cos }^2}\theta }} \\
   \Rightarrow y = \dfrac{{2{b^2}a}}{{{b^2}{{\cos }^2}\theta + {a^2}{{\cos }^2}\theta }} \\
   \Rightarrow y = \dfrac{1}{{2a}} \times \dfrac{{4{a^2}{b^2}}}{{{b^2}{{\cos }^2}\theta + {a^2}{{\sin }^2}\theta }} \\
\]
From equation (1), we have
\[
   \Rightarrow y = \dfrac{1}{{2a}}{x^2} \\
  \therefore {x^2} = 2ay{\text{ or }}\dfrac{{2a}}{x} = \dfrac{x}{y} \\
\]
By converting these into ratio and proportion, we get
\[2a:x\] is in proportion to \[x:y\]
i.e., the length of any focal chord of a conic is third proportional to the transverse axis and the diameter parallel to that chord.
Hence proved.

Note: The general equation of a conic is given by \[\dfrac{l}{r} = 1 - e\cos \theta \] where \[e\] is the eccentricity of the conic. Here the point \[S\] is the focus of the conic. The transverse axis is the axis of the conic that passes through the two foci.