Question

Show that the function $g\left( x \right)=\cos x$ is differentiable at any $a\in \mathbb{R}$ and $g'\left( a \right)=-\sin a.$ In general, $g'\left( x \right)=-\sin x$.

Answer 1

Hint: To check the differentiability of a function, we will find the derivative of the function. To find the derivative of any function $f\left( x \right)$, we will use the first principle of derivative.

Complete step-by-step answer:
 In this question, we are given a function; \[g\left( x \right)=\sin x\].
Since we have to check for the differentiability of this function, we have to first find its derivative. To find the derivative of the function $g\left( x \right)$, we will differentiate $g\left( x \right)$ using the first principle of derivative.
According to first principle, we can find derivative $g'\left( x \right)$ of the function$g\left( x \right)$ using the formula;
$g'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{g\left( x+h \right)-g\left( x \right)}{h}.........\left( I \right)$
Substituting $g\left( x \right)=\cos x$ and $g\left( x+h \right)=\cos \left( x+h \right)$ in the formula $\left( I \right)$, we get;
\[g'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\cos \left( x+h \right)-\cos x}{h}.........\left( II \right)\]
In trigonometry, we have a formula; $\cos \left( x+h \right)=\cos x\cos h-\sin x\sin h$
Substituting this formula i.e. $\cos \left( x+h \right)=\cos x\cos h-\sin x\sin h$ in $\left( II \right)$, we get;
\[\begin{align}
  & \Rightarrow g'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\cos x\cos h-\sin x\sin h-\cos x}{h} \\
 & \Rightarrow g'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\cos x\cos h-\cos x}{h}-\dfrac{\sin x\sin h}{h} \\
\end{align}\]
Since the limit can be distributed over subtraction of the two functions, we can write;
\[\Rightarrow g'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\cos x\left( \cos h-1 \right)}{h}-\underset{h\to 0}{\mathop{\lim }}\,\sin x\dfrac{\sin h}{h}\]
Since the limit is applied on $h$, we can take the functions of$x$out of the individual limits.
$\Rightarrow g'\left( x \right)=\cos x\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\cos h-1}{h}-\sin x\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\sin h}{h}........\left( III \right)$
We have two formulas of limit, $\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\cos h-1}{h}=0$ and $\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\sin h}{h}=1$ .
Substituting $\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\cos h-1}{h}=0$ and $\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\sin h}{h}=1$in equation $\left( III \right)$, we get;
$\begin{align}
  & \Rightarrow g'\left( x \right)=\cos x\left( 0 \right)-\sin x\left( 1 \right) \\
 & \Rightarrow g'\left( x \right)=0-\sin x \\
 & \Rightarrow g'\left( x \right)=-\sin x \\
\end{align}$
It will be easier to check the differentiability of $g\left( x \right)$ if we draw the graph of $g'\left( x \right)=\left( -\sin x \right)$.
Plotting the graph of $g'\left( x \right)=\left( -\sin x \right)$;

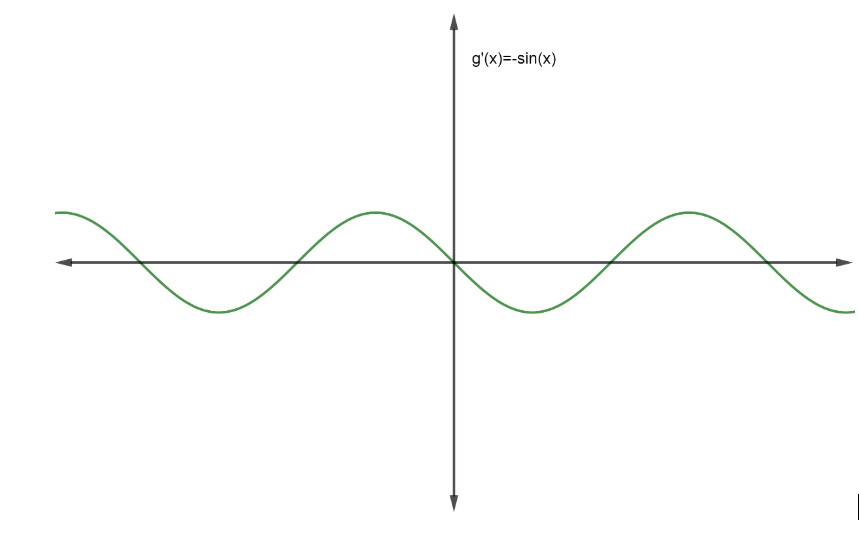
Since the graph of $g'\left( x \right)$ is continuous $\forall x\in \mathbb{R}.$, we can say $g\left( x \right)$ is differentiable$\forall x\in \mathbb{R}.$.
Also, $g'\left( x \right)=-\sin x$. Hence, substituting $x=a$ in $g'\left( x \right)=-\sin x$, we obtain;
$\text{g}'\left( a \right)=-\sin a$

Note: The question can be done directly if one has remembered that the derivatives of $g\left( x \right)=\cos x$ instead of applying the first principle and to finding the value of $g'\left( x \right)$ which may make this question a time taking one.