Question

Show that the function $f\left( x \right)=\sin x$ is differentiable at any $a\in \mathbb{R}$ and $f'\left( a \right)=\cos a.$ In general, $f'\left( x \right)=\cos x$ for $x\in \mathbb{R}$.

Answer 1

Hint: To check the differentiability, we will find the derivative of the function. To find the derivative of the function $f\left( x \right)$ , we will use the first principle of derivative and then use the information provided about the function in the question.

Complete step-by-step answer:
It is given in the question, a function \[f\left( x \right)=\sin x\].
Since we have to check for differentiability of this function, we have to first find its derivative. To find the derivative, we use first principle from which the derivative $f'\left( x \right)$ of a function $f\left( x \right)$ is given by;
$f'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{f\left( x+h \right)-f\left( x \right)}{h}$
For \[f\left( x \right)=\sin x\] and \[f\left( x+h \right)=\sin \left( x+h \right)\], we get;
$\Rightarrow f'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\sin \left( x+h \right)-\sin x}{h}.........\left( I \right)$
We have a formula, $\sin \left( x+h \right)=\sin x\cos h+\cos x\sin h.........\left( II \right)$
Substituting $\sin \left( x+h \right)=\sin x\cos h+\cos x\sin h$ from equation $\left( II \right)$ in equation $\left( I \right)$, we get;
\[\Rightarrow f'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\sin x\cos h+\cos x\sin h-\sin x}{h}\]
Since limit can be distributed over addition of two functions, we can write;
\[\begin{align}
  & \Rightarrow f'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\left( \sin x\cos h-\sin x \right)}{h}+\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\cos x-\sin h}{h} \\
 & \Rightarrow f'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\left( \sin x \right)\left( \cos h-1 \right)}{h}+\underset{h\to 0}{\mathop{\lim }}\,\cos x\dfrac{\sin h}{h} \\
\end{align}\]
Since the limit is applied with respect to $h$, the functions having $x$ can be taken out of the limit.
$\Rightarrow f'\left( x \right)=\sin x\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\left( \cos h-1 \right)}{h}+\cos x\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\sin h}{h}........\left( III \right)$
Also, we have to formulas of limit; $\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\left( \cos h-1 \right)}{h}=0$ and $\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\sin h}{h}=1$.
Substituting $\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\left( \cos h-1 \right)}{h}=0$ and $\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\sin h}{h}=1$ in equation $\left( III \right)$, we get;

$\begin{align}
  & \Rightarrow f'\left( x \right)=\sin x\left( 0 \right)+\cos x\left( 1 \right) \\
 & \Rightarrow f'\left( x \right)=0+\cos x \\
 & \Rightarrow f'\left( x \right)=\cos x \\
\end{align}$
It will be easier to check the differentiability at all the points in the domain of the function i.e. $x\in R$ if we draw the graph of $f'\left( x \right)$ i.e. $\cos x$.
Plotting the graph of $f'\left( x \right)=\cos x$;

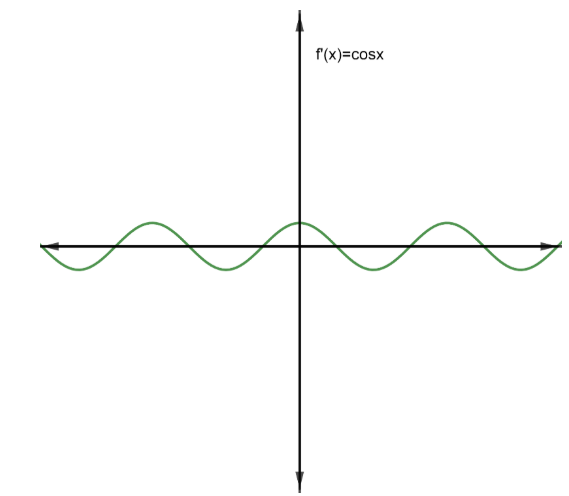
Since the graph of $f'\left( x \right)$ is continuous everywhere, we can say $f\left( x \right)$ is differentiable $\forall x\in \mathbb{R}.$.
Also, in $f'\left( x \right)=\cos x$, if we substitute $x=a$, then we get;
$f'\left( a \right)=\cos a$

Note: The question can be done directly if one had remembered that the derivative of $\sin x$ is $\cos x$ instead of calculating the derivative using the first principle of derivative which actually makes the question a time taking one.