Question

Show that the following set of curves intersect orthogonally.
$y = {x^3}$ and $6y = 7 - {x^2}$

Answer 1

Hint: Here, we are given two curves and to prove that they intersect each other orthogonally, we need to prove that the angle between them is $90^\circ $. For finding the angle between two curves, we will be using the formula
$ \Rightarrow \tan \theta = \left| {\dfrac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}} \right|$, where ${m_1}$ and ${m_2}$ are the slopes.

Complete step by step solution:
In this question, we are given two curves $y = {x^3}$ and $6y = 7 - {x^2}$ and we need to prove that they intersect orthogonally.
Now, if two curves are orthogonal, then the angles between them is always equal to $90^\circ $. That means we need to prove that the angle between the curves $y = {x^3}$ and $6y = 7 - {x^2}$ is $90^\circ $.
For finding the angle, we have the formula
$ \Rightarrow \tan \theta = \left| {\dfrac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}} \right|$ - - - - - - - (1)
And as we know, that slope is given by
$ \Rightarrow Slope\left( m \right) = \dfrac{{dy}}{{dx}}$
Now, first of all, we need to find the values of x and y. For that substitute $y = {x^3}$ in $6y = 7 - {x^2}$. Therefore, we get
$
   \Rightarrow 6\left( {{x^3}} \right) = 7 - {x^2} \\
   \Rightarrow 6{x^3} + {x^2} - 7 = 0 \\
 $
On solving the above equation, we get
$ \Rightarrow x = 1$
And $y = {x^3}$. Therefore,
$
   \Rightarrow y = {\left( 1 \right)^3} \\
   \Rightarrow y = 1 \\
 $
Therefore, the intersecting point is $P\left( {1,1} \right)$.
Now,
$
   \Rightarrow y = {x^3} \\
   \Rightarrow \dfrac{{dy}}{{dx}} = 3{x^2} \\
   \Rightarrow {m_1} = 3{x^2} \\
 $
Now, value of ${m_1}$ at point $P\left( {1,1} \right)$ will be
$ \Rightarrow {m_1} = 3{\left( 1 \right)^2} = 3$
And
$
   \Rightarrow 6y = 7 - {x^2} \\
   \Rightarrow 6\dfrac{{dy}}{{dx}} = 0 - 2x \\
   \Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{{ - 2x}}{6} = \dfrac{{ - x}}{3} \\
   \Rightarrow {m_2} = \dfrac{{ - x}}{3} \\
 $
Now, value of ${m_2}$ at point $P\left( {1,1} \right)$ will be
$ \Rightarrow {m_2} = \dfrac{{ - 1}}{3}$
Therefore, using equation (1), we get
$
   \Rightarrow \tan \theta = \left| {\dfrac{{3 - \left( {\dfrac{{ - 1}}{3}} \right)}}{{1 + \left( 3 \right)\left( {\dfrac{{ - 1}}{3}} \right)}}} \right| \\
   \Rightarrow \tan \theta = \left| {\dfrac{{\dfrac{{10}}{3}}}{{1 - 1}}} \right| \\
   \Rightarrow \tan \theta = \left| {\dfrac{{10}}{0}} \right| \\
   \Rightarrow \tan \theta = \infty \\
 $
Now, we know that the value of $\tan \theta $ is $\infty $ when the value of $\theta $ is equal to $\dfrac{\pi }{2}$. Therefore,
$ \Rightarrow \theta = 90^\circ $
Hence, the angle between the curves $y = {x^3}$ and $6y = 7 - {x^2}$ is $90^\circ $. Hence, we can say that the curves $y = {x^3}$ and $6y = 7 - {x^2}$ intersect each other orthogonally.
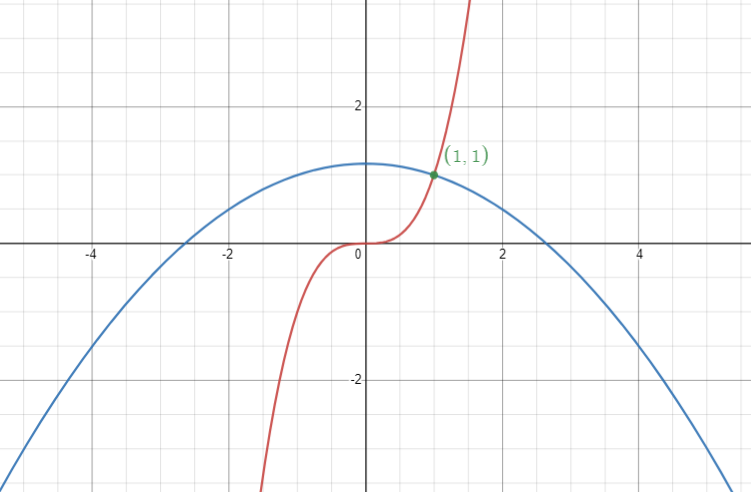
The below graph shows the orthogonal intersection of $y = {x^3}$ (Red curve) and $6y = 7 - {x^2}$ (Blue curve) at (1,1).

Note:
Here, to prove that the curves are orthogonal, the angle must be equal to $90^\circ $. Now, in the formula $\tan \theta = \left| {\dfrac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}} \right|$, $\theta $ will be equal to 90 only when we get $\infty $. And for that the denominator must be equal to 0. So, instead of solving the whole term, we can take
$ \Rightarrow 1 + {m_1}{m_2} = 0$
If the above condition is satisfied, the curves will be orthogonal.