Question

Show that the equation of the line passing through the origin and making an angle $\theta $ with the line $y = mx + c$ is $\dfrac{y}{x} = \dfrac{{m \pm \tan \theta }}{{1 \mp m\tan \theta }}$.

Answer 1

Hint- In this question, we have to find the equation of line passing through origin and making angle $\theta $ with the given line. Proceed with using formula of angle $\theta $ between two lines of different slopes $({m_1},{m_2})$ i.e. $\tan \theta = \left| {\dfrac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}} \right|$ and find a relation between variables x and y to reach the answer.

Complete step-by-step solution -

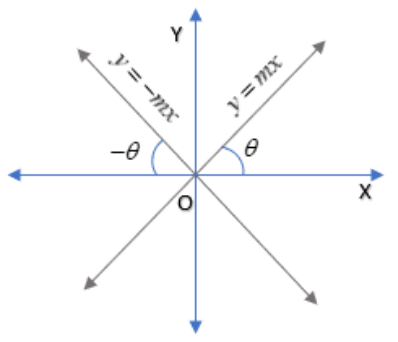
Let equation of the line passing through origin be $y = {m_1}x$ ------(a)
Now, this line makes an angle $\theta $ with the line $y = mx + c$
$ \Rightarrow \tan \theta = \left| {\dfrac{{{m_1} - m}}{{1 + {m_1}m}}} \right|$
Put ${m_1} = \dfrac{y}{x}$ using the equation (a)
$ \Rightarrow \tan \theta = \pm \left( {\dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x} \times m}}} \right)$
From this we get, either $\tan \theta = \left( {\dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x} \times m}}} \right)$ or $\tan \theta = - \left( {\dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x} \times m}}} \right)$
Taking into consideration, $\tan \theta = \left( {\dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x} \times m}}} \right)$
On cross multiplying we get, $\tan \theta \left( {1 + \dfrac{y}{x} \times m} \right) = \dfrac{y}{x} - m$
$ \Rightarrow \tan \theta + \tan \theta \times \dfrac{y}{x} \times m = \dfrac{y}{x} - m$
$ \Rightarrow \tan \theta + m = \dfrac{y}{x} - \tan \theta \times \dfrac{y}{x} \times m$
$ \Rightarrow \tan \theta + m = \dfrac{y}{x}\left( {1 - m\tan \theta } \right)$
$ \Rightarrow \dfrac{{m + \tan \theta }}{{1 - m\tan \theta }} = \dfrac{y}{x}$
or, $\dfrac{y}{x} = \dfrac{{m + \tan \theta }}{{1 - m\tan \theta }}$ ------(b)

Taking into consideration, $\tan \theta = - \left( {\dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x} \times m}}} \right)$
On cross multiplying we get, $\tan \theta \left( {1 + \dfrac{y}{x} \times m} \right) = - \dfrac{y}{x} + m$
$ \Rightarrow \tan \theta + \tan \theta \times \dfrac{y}{x} \times m = - \dfrac{y}{x} + m$
$ \Rightarrow \tan \theta - m = - \dfrac{y}{x} - \tan \theta \times \dfrac{y}{x} \times m$
$ \Rightarrow \tan \theta - m = \dfrac{y}{x}\left( { - 1 - m\tan \theta } \right)$
$ \Rightarrow \dfrac{{\tan \theta - m}}{{ - 1 - m\tan \theta }} = \dfrac{y}{x}$
or, $\dfrac{y}{x} = \dfrac{{m - \tan \theta }}{{1 + m\tan \theta }}$ ------(c)

From (b) and (c) we get,
$\dfrac{y}{x} = \dfrac{{m + \tan \theta }}{{1 - m\tan \theta }}$ or $\dfrac{y}{x} = \dfrac{{m - \tan \theta }}{{1 + m\tan \theta }}$
Collectively we can say that,
$\dfrac{y}{x} = \dfrac{{m \pm \tan \theta }}{{1 \mp m\tan \theta }}$
Hence it has been shown that $\dfrac{y}{x} = \dfrac{{m \pm \tan \theta }}{{1 \mp m\tan \theta }}$.

Note- Always remember for lines passing through origin, the intercept on y-axis is zero and so in equation $y = mx + c,c = 0$ . It can be seen that the line passing through origin can be rewritten as $y = mx$ where m can be negative or positive depending on the angle.